Descripción del ejercicio
En este apartado, construiremos una escena que muestre un cubo compuesto por varios bloques generados aleatoriamente. Debemos incluir un texto que pregunte por el número de bloques y otro texto que muestre “correcto” o “incorrecto”, según la respuesta.
Tamaño de la escena. Debemos cambiar las dimensiones de la escena a 600×400.
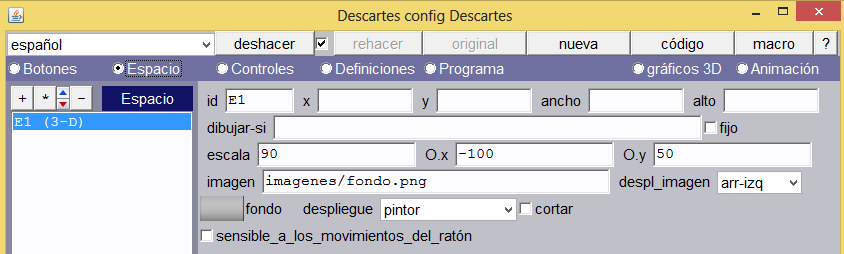
Espacio de trabajo. Insertaremos un espacio 3D con las características que se observan en la imagen de abajo. Asignamos 50 al desplazamiento en y (0.y = 50), -100 al desplazamiento en x (O.x = -100), escala de 90, despliegue pintor y una imagen de fondo.
Controles. Usaremos tres controles.
Control de escala. El programa Descartes trae un control de escala que usaremos en otra sesión. Por ahora añadimos, al interior de la escena, un control numérico tipo barra identificado por la letra a (id) y de nombre Escala. El valor inicial es de 1.5, incremento de 0.1, mínimo 1.5 y máximo 3, con posición en el sur (parte inferior de la escena).
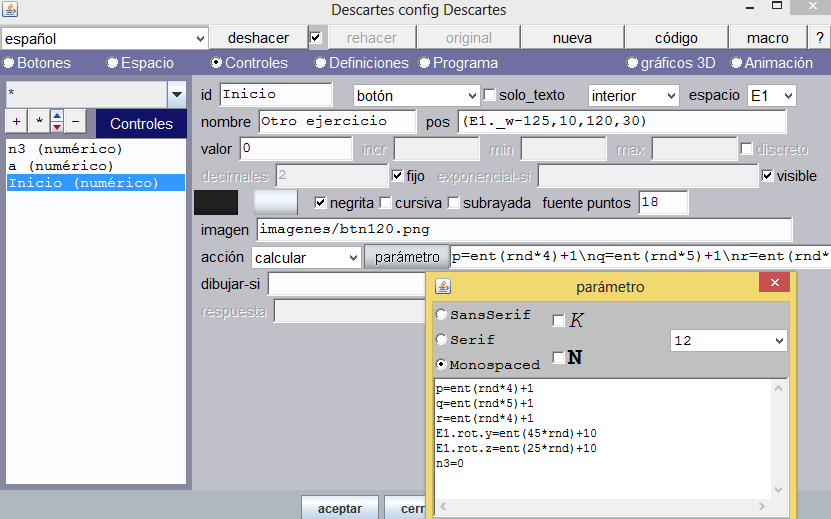
Control de inicio. Añadimos un control numérico tipo botón con el siguiente nombre “Otro ejercicio”, con posición y tamaño definidos por (E1._w-125, 10, 120,30) y cuya acción será similar a la de inicio; sin embargo, el efecto es recalcular las variables usadas en la escena, de tal forma que se reinicie.
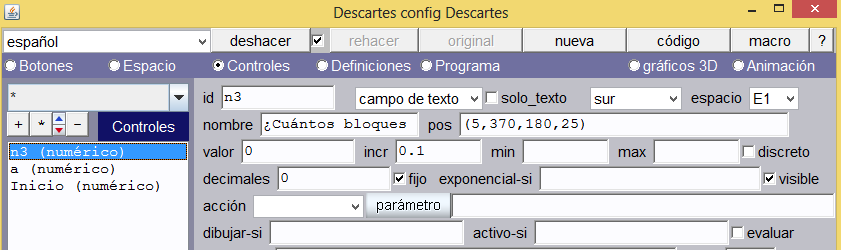
Control para pregunta. Insertamos un control numérico tipo campo de texto cuya posición, como en el primer control, será en el sur de la escena. El nombre de este control es “¿cuántos bloques hay?” Su identificación (id) será n3 (ver imagen siguiente).
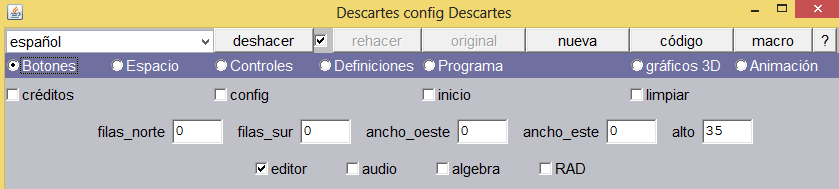
Es importante modificar el alto de los controles que se ubican en la parte inferior de la escena, para facilitar la interacción en dispositivos móviles. Para ello, en la opción botones, hacemos el cambio como se indica en la siguiente imagen:
Algoritmo de inicio. Usaremos cinco variablesr, cuyos valores iniciales son números aleatorios. Si bien el cubo es un paralelepípedo que tiene sus tres dimensiones iguales, generaremos tres variables que harán variar las divisiones en cada uno de los lados del cubo. Para este efecto, hablaremos de largo, ancho y alto.
- Largo. Definido por p = ent(rnd*4)+1. La usaremos para generar aleatoriamente el número de divisiones que tendrá el largo del cubo. Varía entre 1 y 4.
- Ancho. Definido por q = ent(rnd*5)+1. La usaremos para generar aleatoriamente el número de divisiones que tendrá el ancho del cubo. Varía entre 1 y 5.
- Alto. Definido por r = ent(rnd*4)+1. La usaremos para generar aleatoriamente el número de divisiones que tendrá la altura del cubo. Varía entre 1 y 4.
Rotaciones del espacio. Otro efecto que añadiremos es la rotación aleatoria del espacio E1. El Nippe Descartes ofrece un parámetro que permite este tipo de rotación.
- E1.rot.z. Permite rotar el espacio E1 alrededor del eje z un número de grados asignados. Por ejemplo, E1.rot.z = 30 lo hará rotar 30 grados.
- E1.rot.y. Permite rotar el espacio E1 alrededor del eje y un número de grados asignados. Por ejemplo, E1.rot.y = 30 lo hará rotar 30 grados.
De acuerdo a lo anterior, insertaremos en el algoritmo de inicio las variables, tal como se indica en la imagen:
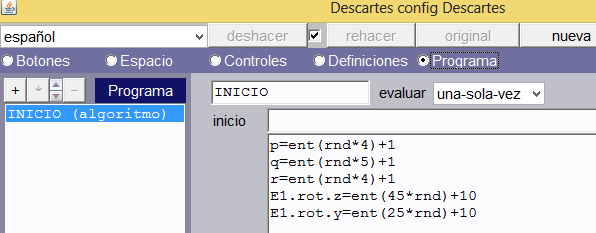
- E1.rot.z = ent(45*rnd)+10. Permite rotar el espacio alrededor del eje z un valor de n grados, donde n varía entre 10 y 54 grados.
- E1.rot.y = ent(25*rnd)+10. Permite rotar el espacio alrededor del eje y un valor de n grados, donde n varía entre 10 y 34 grados.
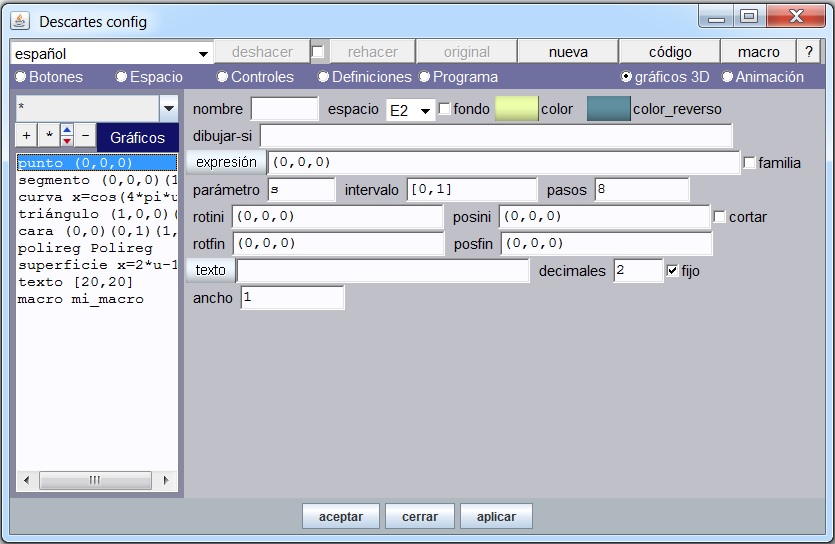
Gráficos 3D. Usaremos seis superficies y tres textos.
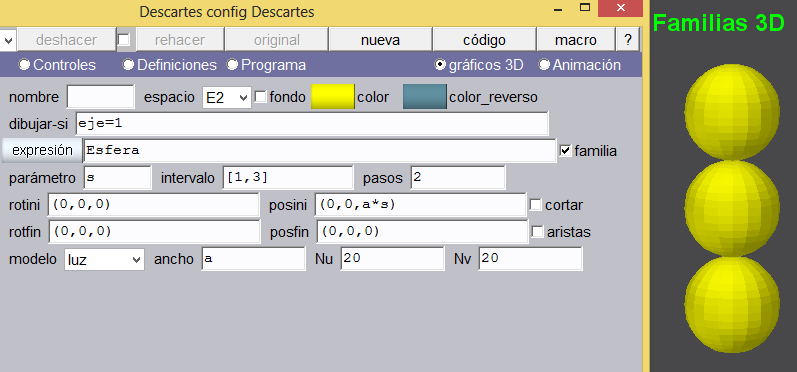
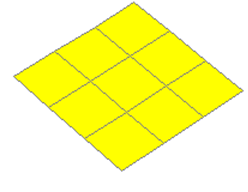 Cara 1 del cubo. Insertamos una superficie cuya expresión es “x=a*u y=a*v z=0”. Es decir, un plano sobre xy. Observemos que el tamaño en que podemos ver el plano depende del factor de escala que llamamos a. Por defecto este plano se dibujaría como la primera imagen de abajo (izquierda). Si activamos las aristas, la imagen cambia (ver imagen central) a un plano dividido por siete líneas en cada uno de sus lados, dado que Nu = 7 y Nv = 7. Si cambiamos estos valores por Nu = p y Nv = q, las aristas variarán aleatoriamente cada vez que hacemos clic en el botón Otro ejercicio. Finalmente, debemos escoger un color para esta cara.
Cara 1 del cubo. Insertamos una superficie cuya expresión es “x=a*u y=a*v z=0”. Es decir, un plano sobre xy. Observemos que el tamaño en que podemos ver el plano depende del factor de escala que llamamos a. Por defecto este plano se dibujaría como la primera imagen de abajo (izquierda). Si activamos las aristas, la imagen cambia (ver imagen central) a un plano dividido por siete líneas en cada uno de sus lados, dado que Nu = 7 y Nv = 7. Si cambiamos estos valores por Nu = p y Nv = q, las aristas variarán aleatoriamente cada vez que hacemos clic en el botón Otro ejercicio. Finalmente, debemos escoger un color para esta cara.
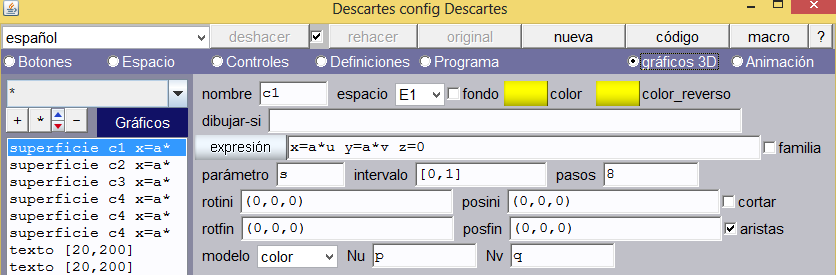
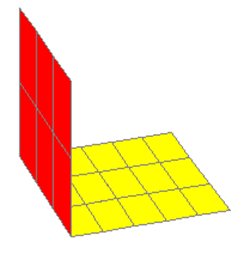 Cara 2 del cubo. Insertamos otra superficie cuya expresión es la de cara anterior. Es decir, expresión: x=a*u y=a*v z=0. La rotaremos 90 grados alrededor del eje x, para ello usamos un rotini de (90, 0, 0). Si observamos la figura del lado derecho comprenderemos lo que estamos haciendo. Para garantizar que las divisiones del lado común sean iguales, usaremos Nu = p (Nu va sobre el eje x). La otra dimensión es el alto del cubo, es decir Nv = r. Terminamos esta cara activando las aristas y usando otro color.
Cara 2 del cubo. Insertamos otra superficie cuya expresión es la de cara anterior. Es decir, expresión: x=a*u y=a*v z=0. La rotaremos 90 grados alrededor del eje x, para ello usamos un rotini de (90, 0, 0). Si observamos la figura del lado derecho comprenderemos lo que estamos haciendo. Para garantizar que las divisiones del lado común sean iguales, usaremos Nu = p (Nu va sobre el eje x). La otra dimensión es el alto del cubo, es decir Nv = r. Terminamos esta cara activando las aristas y usando otro color.
Cara 3 del cubo. Insertamos una superficie igual a la anterior. Lo único que cambiaremos es su posición a un posini de (0, a, 0). De esa manera creamos una cara paralela a la anterior. Activa aristas y cambia color.
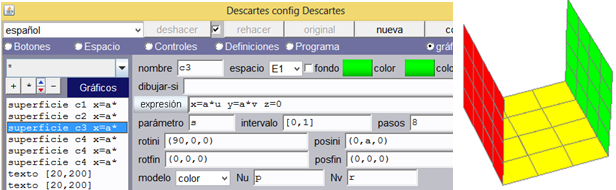
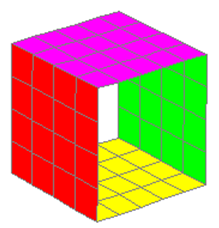 Cara 4 del cubo. Insertamos una superficie igual a la anterior cambiando posini a (0, 0, a) y rotini a (0, 0, 0). De esa manera creamos la cara superior del cubo. Como esta cara es paralela a la primera, entonces Nu = p y Nv = q. Activamos aristas y cambiamos el color.
Cara 4 del cubo. Insertamos una superficie igual a la anterior cambiando posini a (0, 0, a) y rotini a (0, 0, 0). De esa manera creamos la cara superior del cubo. Como esta cara es paralela a la primera, entonces Nu = p y Nv = q. Activamos aristas y cambiamos el color.
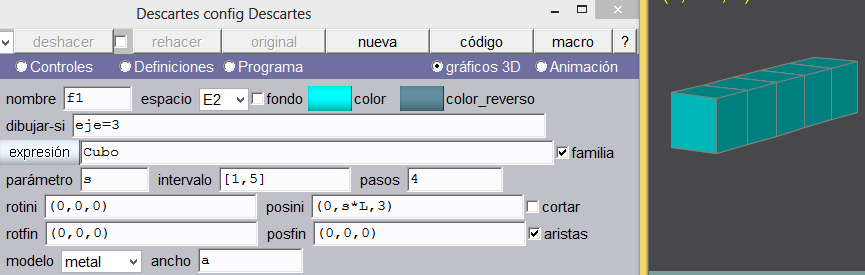
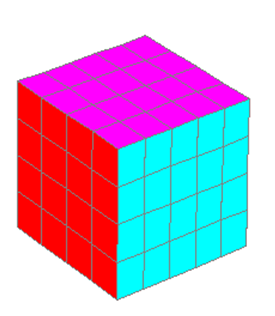 Cara 5 del cubo. Insertamos una superficie con expresión igual a las anteriores. Es decir x=a*u y=a*v z=0. Para esta cara veremos la utilidad de lo que aprendimos en la clase 13. La cara inicial es la de color amarillo de la imagen derecha. La cara de color rojo es la segunda cara que agregamos. La cara que vamos a agregar es la de color magenta. Para lograr esta cara debemos desplazar la amarilla a lo largo del eje x con un posini de (a, 0, 0) y rotarla alrededor del eje y con un rotini de (0, -90, 0). Nu = r y Nv = q ¿por qué?
Cara 5 del cubo. Insertamos una superficie con expresión igual a las anteriores. Es decir x=a*u y=a*v z=0. Para esta cara veremos la utilidad de lo que aprendimos en la clase 13. La cara inicial es la de color amarillo de la imagen derecha. La cara de color rojo es la segunda cara que agregamos. La cara que vamos a agregar es la de color magenta. Para lograr esta cara debemos desplazar la amarilla a lo largo del eje x con un posini de (a, 0, 0) y rotarla alrededor del eje y con un rotini de (0, -90, 0). Nu = r y Nv = q ¿por qué?
Activamos aristas y usamos otro color.
Cara 6 del cubo. Esta cara es igual a la anterior (cara opuesta) con posini (0, 0, 0). Activamos aristas y usamos otro color.
Texto 1. Este texto escribirá el mensaje “¡Correcto!” cuando n3 = p*q*r, que ubicaremos en [20, 200]. Observemos en la imagen de abajo un ejemplo de la escena.
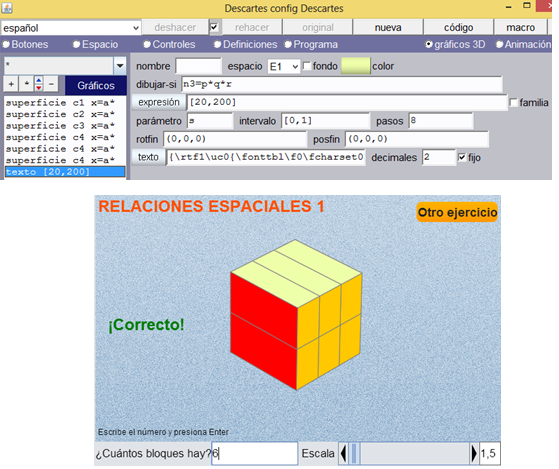
Texto 2. Este texto escribirá el mensaje “¡Incorrecto!” cuando n3 es diferente de p*q*r y mayor que cero (esta última condición, para evitar que aparezca al inicio de la escena). Lo ubicaremos en [20, 150]. El programa Descartes representa el símbolo de “diferente” con la combinación de estos dos símbolos !=. De acuerdo con lo anterior, el texto aparecerá cuando esta condición sea verdadera: dibujar-si = (n3!=p*q*r)&(n3>0).
Texto 3. Este texto escribirá el mensaje “Escribe el número y presiona ENTER” en la posición [5, 360].
Texto 4. Un título para la escena, similar al que aparece en la escena final:
EJERCICIOS
Con lo aprendido anteriormente, proponemos realizar ejercicios más complejos, como los que se describen a continuación:
Ejercicio 1. Construir una escena que muestre un cubo compuesto por varios bloques generados aleatoriamente. Las divisiones del alto deben ser iguales a las del largo. La escena final que se espera es la siguiente:
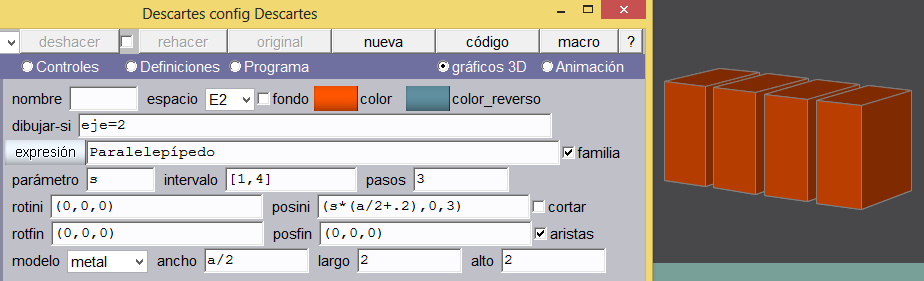
Ejercicio 2. Construir una escena que muestre un cubo compuesto por varios bloques generados aleatoriamente y un paralelepípedo compuesto, también de bloques aleatorios, ubicados sobre la cara superior del cubo. El alto del paralelepípedo no tiene divisiones.
Ejercicio 3. Construir una escena que muestre un cubo compuesto por varios bloques generados aleatoriamente. Las divisiones del alto son sólo dos. De la división superior se deben restar algunos bloques.
Puede descargarse todas las escenas anteriores desde este enlace.
¡Eso es todo!
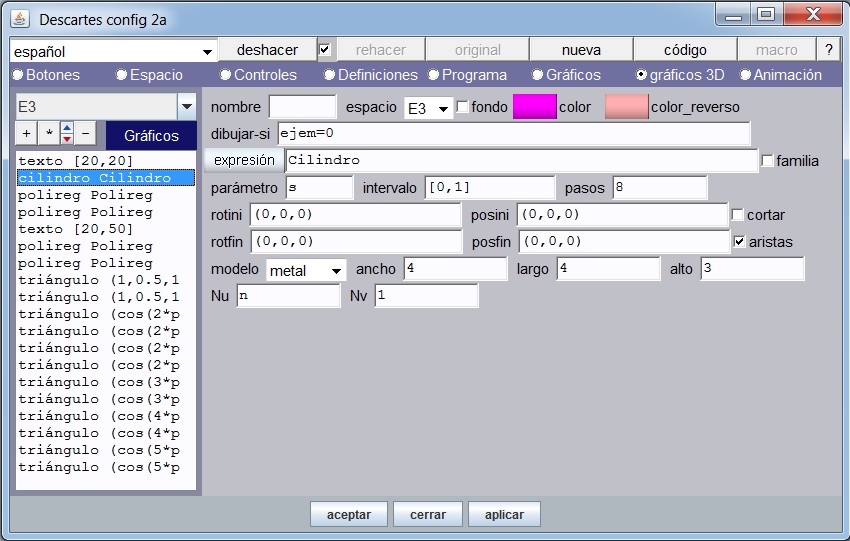





 Cara 1 del cubo. Insertamos una superficie cuya expresión es “x=a*u y=a*v z=0”. Es decir, un plano sobre xy. Observemos que el tamaño en que podemos ver el plano depende del factor de escala que llamamos a. Por defecto este plano se dibujaría como la primera imagen de abajo (izquierda). Si activamos las aristas, la imagen cambia (ver imagen central) a un plano dividido por siete líneas en cada uno de sus lados, dado que Nu = 7 y Nv = 7. Si cambiamos estos valores por Nu = p y Nv = q, las aristas variarán aleatoriamente cada vez que hacemos clic en el botón Otro ejercicio. Finalmente, debemos escoger un color para esta cara.
Cara 1 del cubo. Insertamos una superficie cuya expresión es “x=a*u y=a*v z=0”. Es decir, un plano sobre xy. Observemos que el tamaño en que podemos ver el plano depende del factor de escala que llamamos a. Por defecto este plano se dibujaría como la primera imagen de abajo (izquierda). Si activamos las aristas, la imagen cambia (ver imagen central) a un plano dividido por siete líneas en cada uno de sus lados, dado que Nu = 7 y Nv = 7. Si cambiamos estos valores por Nu = p y Nv = q, las aristas variarán aleatoriamente cada vez que hacemos clic en el botón Otro ejercicio. Finalmente, debemos escoger un color para esta cara.
 Cara 2 del cubo. Insertamos otra superficie cuya expresión es la de cara anterior. Es decir, expresión: x=a*u y=a*v z=0. La rotaremos 90 grados alrededor del eje x, para ello usamos un rotini de (90, 0, 0). Si observamos la figura del lado derecho comprenderemos lo que estamos haciendo. Para garantizar que las divisiones del lado común sean iguales, usaremos Nu = p (Nu va sobre el eje x). La otra dimensión es el alto del cubo, es decir Nv = r. Terminamos esta cara activando las aristas y usando otro color.
Cara 2 del cubo. Insertamos otra superficie cuya expresión es la de cara anterior. Es decir, expresión: x=a*u y=a*v z=0. La rotaremos 90 grados alrededor del eje x, para ello usamos un rotini de (90, 0, 0). Si observamos la figura del lado derecho comprenderemos lo que estamos haciendo. Para garantizar que las divisiones del lado común sean iguales, usaremos Nu = p (Nu va sobre el eje x). La otra dimensión es el alto del cubo, es decir Nv = r. Terminamos esta cara activando las aristas y usando otro color.
 Cara 4 del cubo. Insertamos una superficie igual a la anterior cambiando posini a (0, 0, a) y rotini a (0, 0, 0). De esa manera creamos la cara superior del cubo. Como esta cara es paralela a la primera, entonces Nu = p y Nv = q. Activamos aristas y cambiamos el color.
Cara 4 del cubo. Insertamos una superficie igual a la anterior cambiando posini a (0, 0, a) y rotini a (0, 0, 0). De esa manera creamos la cara superior del cubo. Como esta cara es paralela a la primera, entonces Nu = p y Nv = q. Activamos aristas y cambiamos el color.  Cara 5 del cubo. Insertamos una superficie con expresión igual a las anteriores. Es decir x=a*u y=a*v z=0. Para esta cara veremos la utilidad de lo que aprendimos en la clase 13. La cara inicial es la de color amarillo de la imagen derecha. La cara de color rojo es la segunda cara que agregamos. La cara que vamos a agregar es la de color magenta. Para lograr esta cara debemos desplazar la amarilla a lo largo del eje x con un posini de (a, 0, 0) y rotarla alrededor del eje y con un rotini de (0, -90, 0). Nu = r y Nv = q ¿por qué?
Cara 5 del cubo. Insertamos una superficie con expresión igual a las anteriores. Es decir x=a*u y=a*v z=0. Para esta cara veremos la utilidad de lo que aprendimos en la clase 13. La cara inicial es la de color amarillo de la imagen derecha. La cara de color rojo es la segunda cara que agregamos. La cara que vamos a agregar es la de color magenta. Para lograr esta cara debemos desplazar la amarilla a lo largo del eje x con un posini de (a, 0, 0) y rotarla alrededor del eje y con un rotini de (0, -90, 0). Nu = r y Nv = q ¿por qué?

Comentarios recientes