Una animación en Descartes es un algoritmo especial que refresca la escena cada vez que realiza un ciclo. Como todo algoritmo tiene la estructura inicio – hacer – mientras.

El Panel de configuración de la Animación tiene este aspecto.

El panel de configuración de la animación tiene estos campos:

Los campos inicio, hacer y mientras funcionan igual que en  cualquier algoritmo.

El siguiente ejemplo muestra una animación que representa una cuerda vibrante blanca con sus primeros armónicos en colores rojo, amarillo, verde, azul y los más altos en violeta. Para distinguir los de color violeta hay que aumentar mucho la amplitud.

Descripción del ejercicio

Realizaremos un ejercicio que nos permitirá comprender cómo se anima una escena. Dicho ejercicio consiste en la construcción de una circunferencia unitaria (circunferencia goniométrica) y sobre ella un punto que se desplazará de acuerdo a un ángulo a que variará de 0 a 2pi Las coordenadas de este punto serán, entonces, (cos(a), sen(a)). Por otra parte, construiremos las funciones seno, coseno, tangente y secante, que serán animadas en función del ángulo a.

Primera animación. Circunferencia unitaria

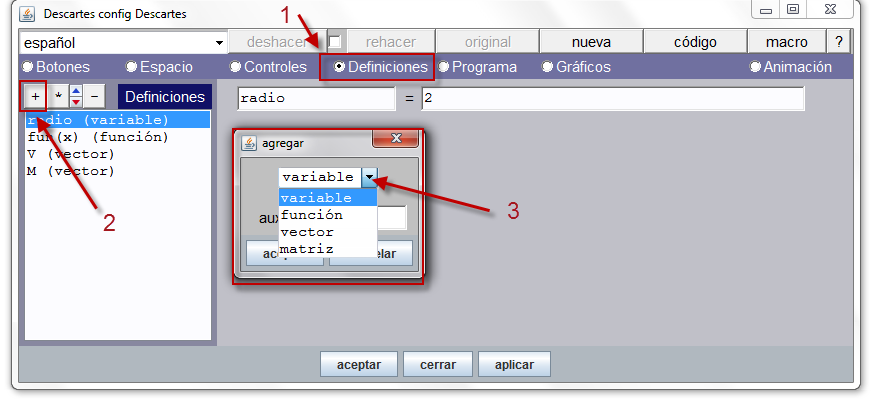
En primer lugar, definiremos el tamaño de la escena en 600×400 píxeles. Para ello, debemos recordar que este cambio se hace pulsando en la opción código.

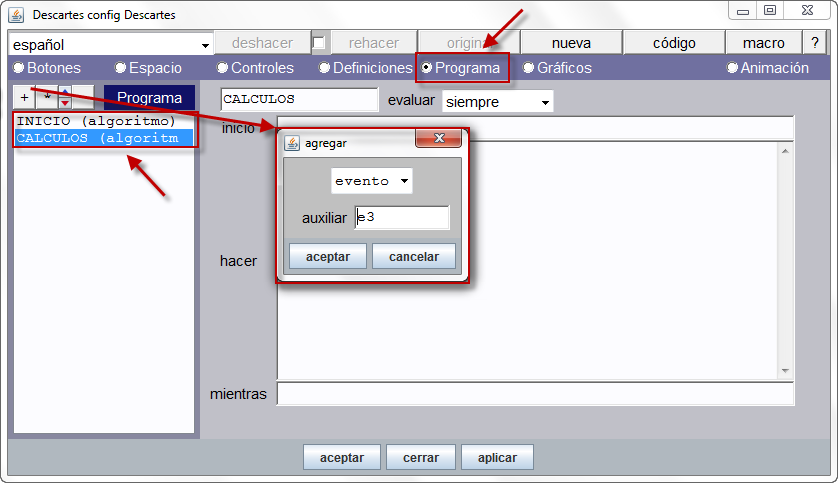
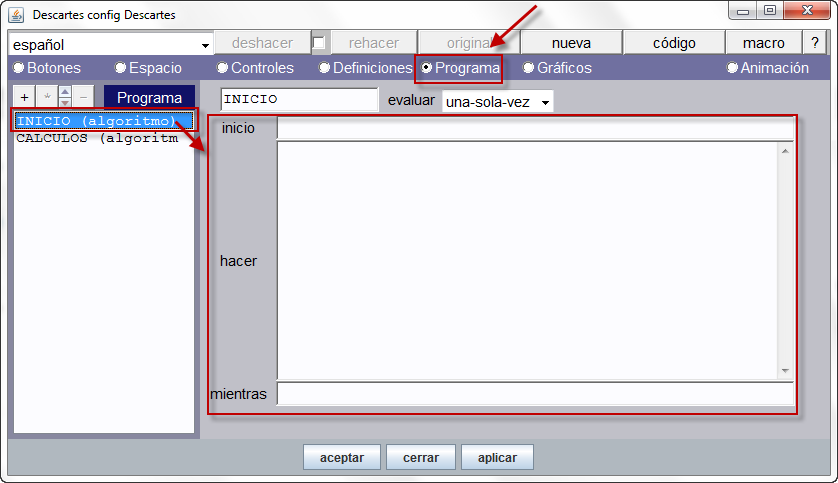
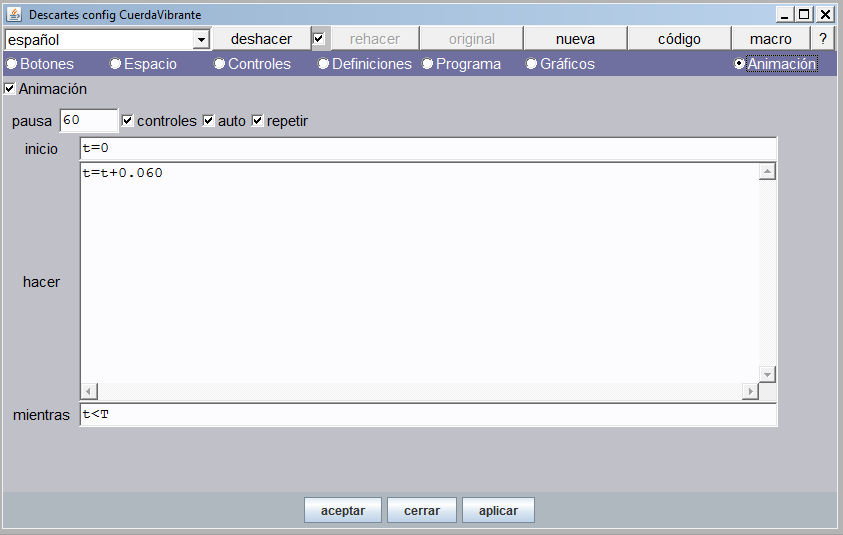
Animación. Ahora, seleccionamos la opción animación, en la que incluiremos los valores que se observan en la imagen. Los valores el algoritmo sólo se pueden digitar si hemos activado la casilla de Animación.

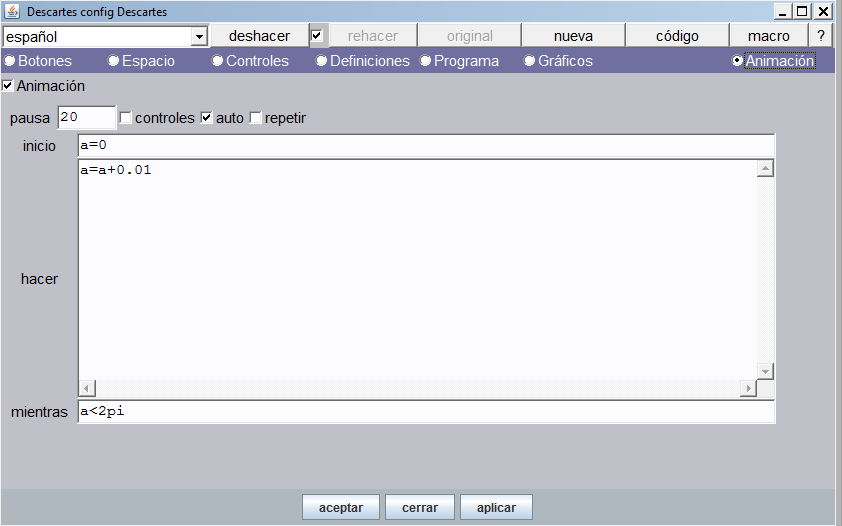
El contenido de la animación tiene la siguiente explicación:

• Pausa. Tiempo de espera entre un paso y otro de la animación. Por defecto está en 60 milésimas de segundo. Usaremos para este ejercicio un valor de 30.
• Inicio. Allí colocaremos nuestro ángulo a con un valor inicial de cero (0) radianes. Es posible “inicializar” varios parámetros separándolos por “;”. Por ejemplo: a=0; r=1;…
• Hacer. Aquí escribimos los cálculos de nuestra animación. En nuestro ejercicio, haremos que el ángulo se incremente en cada paso una centésima. Podríamos practicar con otros incrementos para observar los efectos sobre la animación.
• Mientras. Aquí escribimos la condición que permite que los pasos de “hacer” se sigan realizando. Es decir, mientras la condición sea verdadera, el ángulo se seguirá incrementando. En nuestro ejercicio la condición es a<2pi.

Circunferencia goniométrica animada.  En la opción gráficos del editor de configuraciones, añadimos la circunferencia unitaria x² + y² = 1, tal como se observa en la imagen.

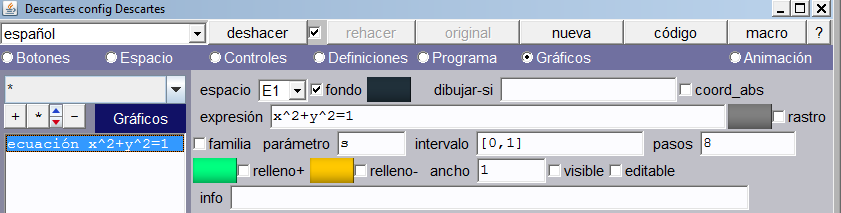
Haremos algunas modificaciones al espacio de trabajo, para efectos de una mejor visualización de la escena. Cambiamos la escala a 75 y la ubicación del origen de coordenadas en O.x = -35%.

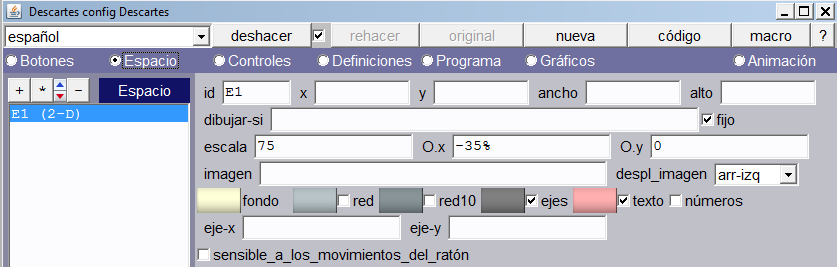
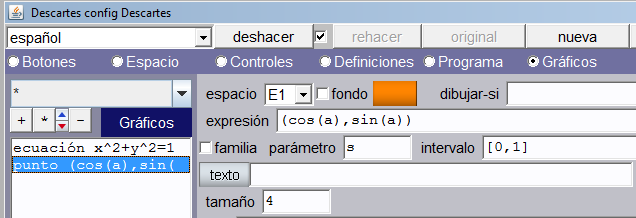
Nuevamente, en gráficos,  añadiremos el siguiente punto: (cos(a), sin(a)), con color rojo y tamaño 5… ¡empieza la animación!

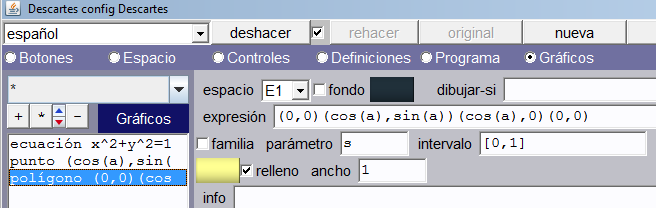
Triángulo trigonométrico animado. Ahora añadimos el siguiente polígono que nos animará el triángulo trigonométrico: (0,0)(cos(a),sin(a))(cos(a),0)(0,0). Observemos que hemos activado el color de relleno (podemos usar el color que deseemos).

Ahora, guardamos, ejecutamos y observamos esta primera animación.

Segunda animación. Funciones trigonométricas animadas

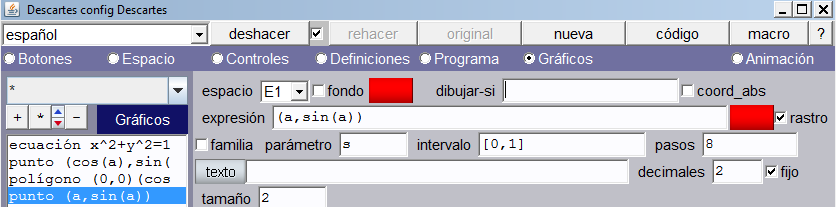
Vamos a animar la función seno añadiendo el siguiente punto (a, sin(a)). Para crear la animación activaremos la opción rastro con el color que queramos. Esta opción permite dejar la huella de los diferentes puntos que se dibujan con (a, sin(a)).

Como tarea, no queda  incluir un control tipo menú para que muestre las demás funciones y un control tipo botón que pause o reanude la animación.

Esta sería la escena final

Hemos  incluido algo adicional, ¿qué es? Observemos la animación.