La anidación de ciclos o bucles es necesaria para hacer determinados procesamientos un poco más complejos que los que realiza un ciclo simple. En Descartes, el ciclo simple es del tipo DO-WHILE (véase http://descartesjs.org/documentacion/?cat=37).
No obstante, existen otras estructuras para definir un ciclo, entre ellas, las de tipo FOR/NEXT. En Javascript, un ciclo anidado tiene una estructura como la que sigue:
for (i=0;i<10;i++){
for (j=0;j<10;j++) {
document.write(i + «-» + j)
}
}
La ejecución de este ejemplo funcionará de la siguiente manera. Para empezar se inicializa el primer ciclo, con lo que la variable i valdrá cero, a continuación se inicializa el segundo ciclo, con lo que la variable j valdrá también cero. En cada iteración se imprime el valor de la variable i, un guión («-«) y el valor de la variable j, como las dos variables valen cero, se imprimirá el texto «0-0» en la página web. Debido al flujo del programa, el ciclo que está anidado es el que más veces se ejecuta; por ejemplo, cuando la variable i toma el valor de uno, se ejecuta el ciclo interno con j desde 0 hasta 10, obteniéndose la siguiente impresión en la web:
1-0
1-1
1-2
1-3
1-4
1-5
1-6
1-7
1-8
1-9
Para cada iteración del ciclo externo se ejecutarán las 10 iteraciones del ciclo interno o anidado.
Siguiendo este estructura, veamos dos ejemplos con Descartes:
Ejemplo 1. Cálculo de los factoriales de los primeros nueve números naturales
El código que resuelve el problema es:
for ( i=1; i < 9; i++) {
Factorial[i]=1
for (j=1; j< i; j++) {
Factorial[i]=Factorial[i]*j
}
}
En el editor de Descartes haríamos lo siguiente:
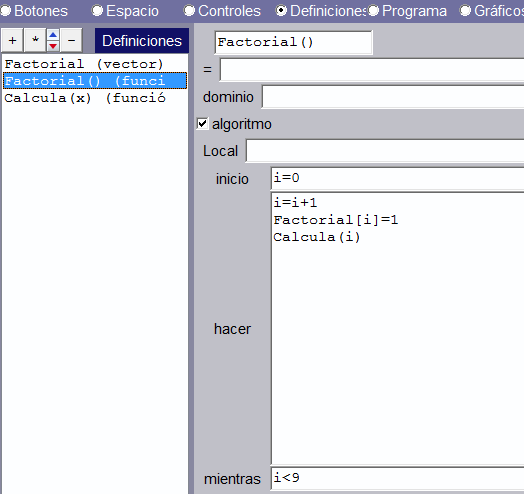
En el algoritmo de INICIO, invocamos la función factorial()
Definimos el vector Factorial, que almacenará los números factoriales:
Creamos el ciclo externo a través de la función Factorial():
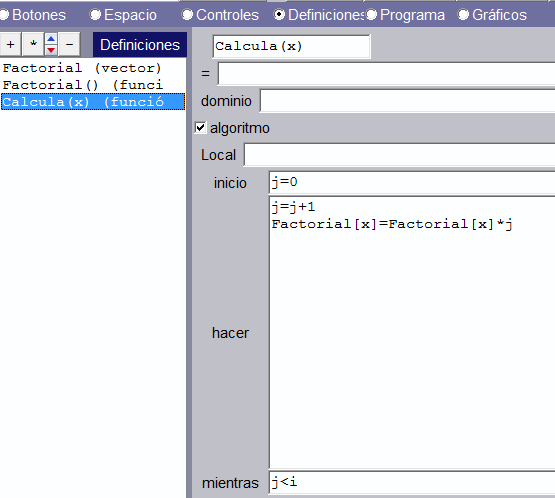
El ciclo externo invoca al ciclo interno, a través de la función Calcula(). Creamos, entonces, este ciclo así:
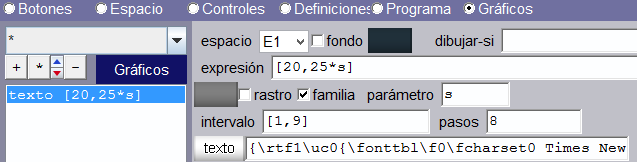
Luego, con una familia de textos, imprimimos el resultado:
Finalmente, ejecutamos y obtenemos:
Ejemplo 2. Algoritmo de ordenamiento y la Mediana
Joel Espinosa Longi propone cuatro tipos de algoritmos de ordenamiento (véase http://proyectodescartes.org/Un_100/materiales_didacticos/_Un_081_AlgoritmosDeOrdenamiento/index.html). Para este ejemplo, hemos escogido el tipo burbuja.
Este algoritmo es útil para algunas aplicaciones; por ejemplo, Si deseamos calcular la mediana de N números dados, almacenados en el vector A, el algoritmo propuesto por Joel, sería:
for (i=0; i<N; i++) {
for (j = 0; j<N-1-i; j++) {
if (A[j] > A[j+1]) {
intercambia(A[j], A[j+1])
}
}
}
En el editor Descartes lo haríamos así:
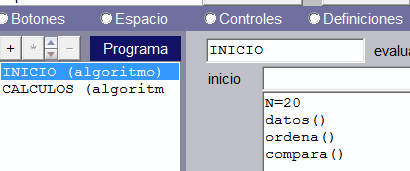
En el algoritmo de INICIO, hemos definido el valor de N e invocado tres funciones, que explicamos a continuación:
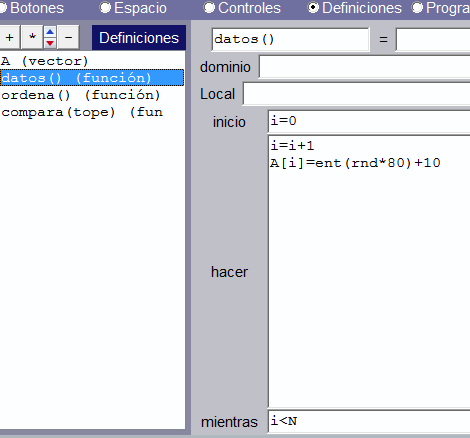
La función datos() se encarga de generar 20 números aleatorios (previamente, definimos el vector A con un tamaño de 21):
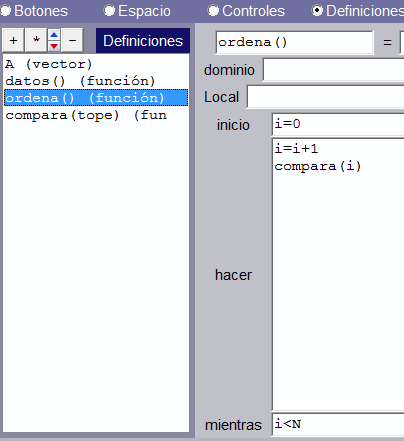
La función ordena() genera el ciclo externo para la variable i, en el que se invoca el ciclo interno compara():
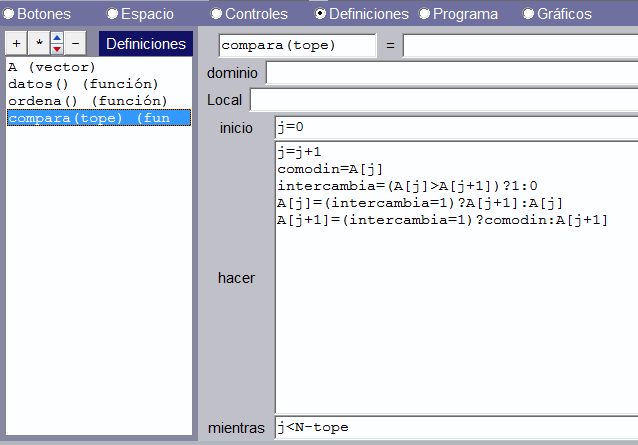
La función compara() se encarga de verificar la condición del algoritmo tipo burbuja, que de cumplirse, realiza el intercambio:
Finalmente, creamos una familia de textos que nos muestra los resultados, uno de ellos es:
Escena de aplicación. A continuación, se presenta una escena interactiva que utiliza el algoritmo anterior:
(Puede descargar esta escena desde este enlace)





Haz un comentario