ILUSIONES ANIMADAS
En este apartado aprenderemos sobre las ilusiones visuales del grupo de investigación sobre la Ciencia Perceptual del Instituto Tecnológico de Massachusetts (MIT) liderado por Edward Adelson.
Perceptual Science Group of the MIT. Este grupo fue creado en 1994 en el Departamento de Ciencias cognitivas y del Cerebro del MIT. El grupo se ha dedicado a la investigación de la percepción visual en brillo y transparencia, percepción de texturas, percepción de superficies, similitud perceptual, análisis de movimiento, entre otras líneas de investigación. El grupo está compuesto por cuatro profesores y un selecto grupo de estudiantes graduados o en curso[1]. Los investigadores principales son Edward Adelson (Profesor de Ciencias de la Visión), Richards Whitman (Profesor de Ciencias Cognitivas), Ruth Rosentholtz (Investigadora) y Aude Oliva (Profesora Asistente en Ciencias Visuales).
La profesora Oliva frente al tema de contexto expresa:
El contexto tiene efectos en múltiples niveles: semántico (una mesa y una silla se hallarán, probablemente en la misma imagen. No esperaríamos una mesa y un elefante), configuración espacial (un teclado se espera observarlo debajo de un monitor) y postura (Las sillas se esperan encontrar dirigidas hacia la mesa, una pluma de escribir esperamos verla en una posición particular respecto al papel y un auto debería estar orientado a los largo de una calle.[2]
Nuestro cerebro tiende a asociar los objetos percibidos con los conocimientos previos adquiridos. El contexto o entorno en el cual se encuentra el objeto hace que nuestro cerebro le asigne propiedades de ese contexto al objeto percibido. Es decir, no percibimos el color y brillo reales, sino los calculados en comparación con el color y brillo de los objetos cercanos (ver la ilusión de Neblina, por ejemplo). En la siguiente imagen, creada por Edward Adelson, las casillas A y B son del mismo tono gris. Diseñaremos un applet que evidencie la igualdad de color.

Algunos demos en flash se han publicado en http://web.mit.edu/persci/gaz/main-frameset.html, de los cuales hemos escogido la ilusión de Haze y el anillo de Koffka para diseñarlos en próximos apartados, pero ahora nos centraremos en la ilusión de Adelson[3].
Las animaciones múltiples en Descartes. El Nippe Descartes trae la opción de animación. En principio parece que sólo podemos realizar una sola animación; sin embargo, usando algunas expresiones de tipo booleano podemos lograr varias animaciones en una sola escena.
La ilusión del tablero ajedrezado
La ilusión de Adelson está compuesta de un tablero de 25 paralelepípedos, un cilindro y una sombra (shadow). El diseño de la escena lo haremos comenzando con la parte gráfica para terminar con las propiedades del espacio, las auxiliares y la animación.
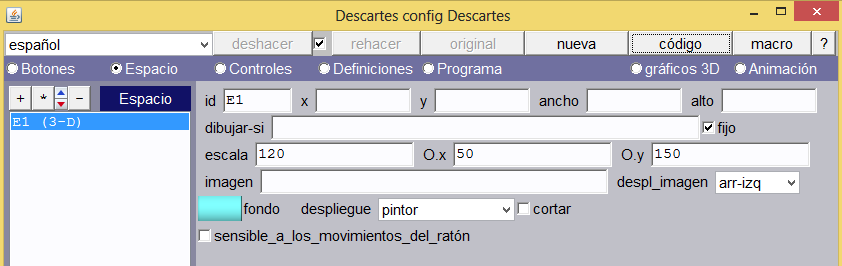
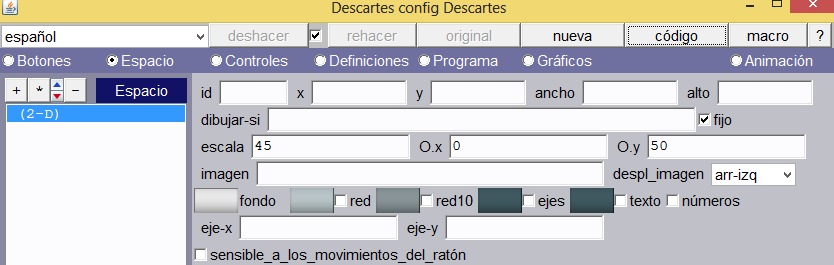
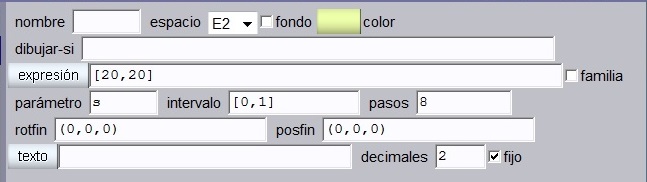
Escena. Inicialmente, crearemos una escena de 550×400, en la que agregaremos, además, un espacio 3D con despliegue pintor y parámetros como los que indica la imagen.
Gráficos. Inciaremos con la creación de los 25 paralelépipedos que se han numerado en la imagen siguiente. En la posición de los paralelépipedos 16, 17, 21 y 22 situaremos el cilindro.

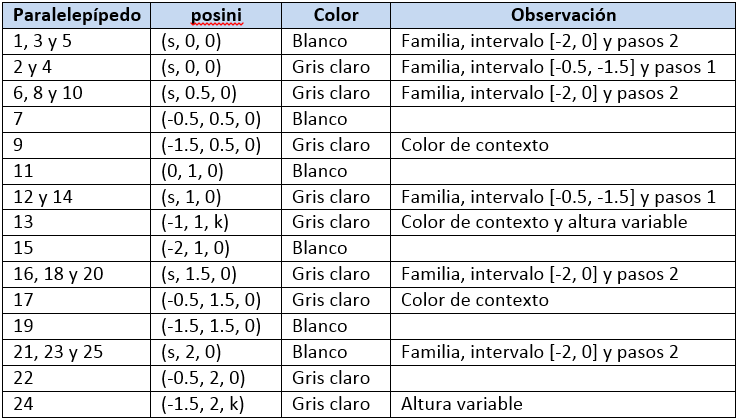
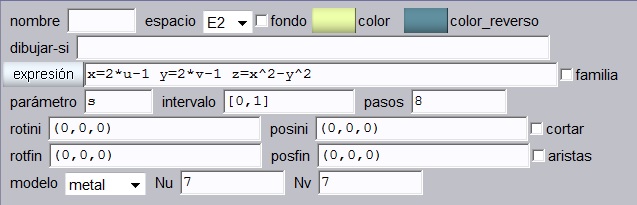
Paralelepípedos. Insertaremos estos prismas en el orden que se presenta en la tabla. Cada paralelepípedo tendrá un ancho y largo de 0.5 y un alto de 0.3, aristas activadas, sus colores serán alternados en gris claro y blanco, excepto en los colores de contexto.
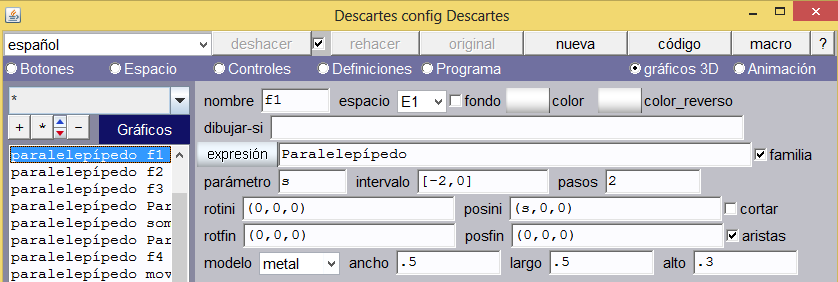
Aprovecharemos, en algunos paralelepípedos, la opción familia, que identificaremos por el posini y la observación; no obstante, debido a la animación, algunos serán construidos individualmente.
Observemos que los paralelepípedos 13 y 24 tendrán una altura variable, estos prismas serán los que animaremos posteriormente.
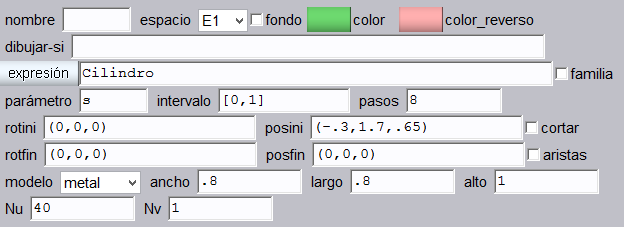
Cilindro. Insertemos un cilindro de color verde claro, ubicado en la posición (-3, 1.7, .65), con ancho y largo de 0.8, Nu = 40 y Nn = 1.
Tapa del cilindro. Añadimos la tapa del cilindro insertando un polígono regular (Polireg) en la posición (-.3, 1.7, 1.15), las demás propiedades de color, ancho, largo, Nu y Nv son iguales a las del cilindro.
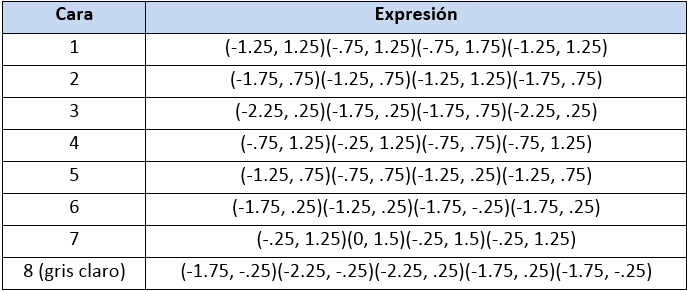
Caras de contexto (sombra). Para emular la sombra del cilindro sobre el tablero, insertaremos siete caras de color gris obscuro y una cara de color gris (extremo izquierdo de la imagen siguiente), cada cara tendrá un posini de (0, 0, 0.15).

Observemos que se trata de siete triángulos negros y un cuadrado gris claro. Analiza aparte las coordenadas de estos cuatro tipos de gráficos (paralelepípedo, polígono regular, cilindro y cara.
Segmentos. Añadimos dos segmentos de color rojo y naranja de acuerdo a las siguientes imágenes:
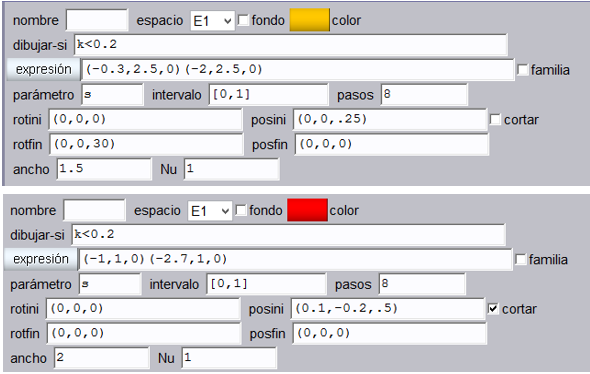
Los segmentos desaparecen cuando k empieza a aumentar en la animación.
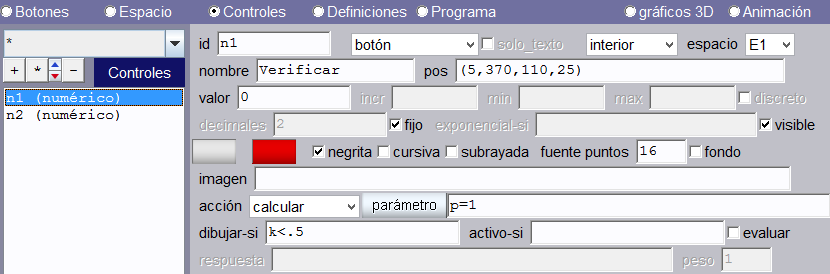
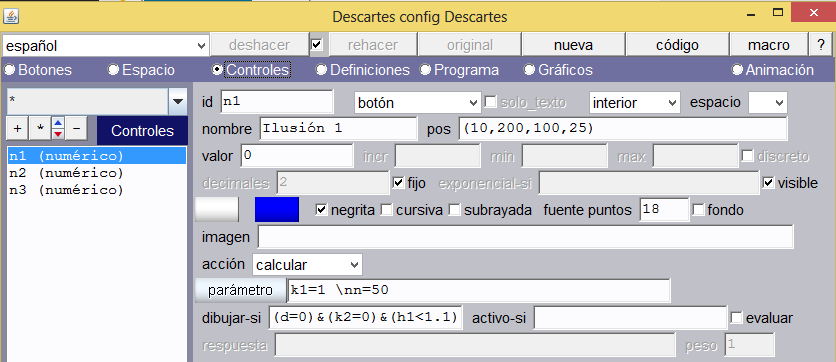
Controles. Usaremos dos controles tipo botón. El primero tendrá como nombre Verificar y demás propiedades como aparecen en la imagen de abajo. El segundo botón tendrá las mismas propiedades excepto: nombre = Regresar, dibujar-si = k > 0.8 y parámetro p = 0. Los colores de los botones los podemos cambiar a nuestro gusto.
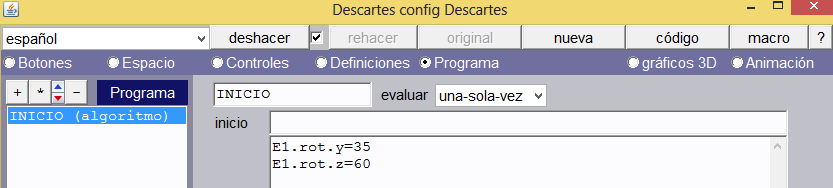
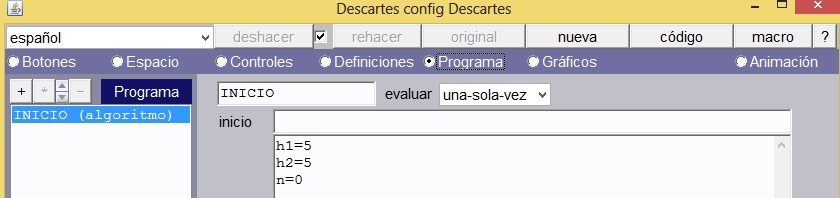
Algoritmo de inicio. Hemos usado dos variables para rotar el espacio E1.rot.y = 35 y E1.rot.z = 60.
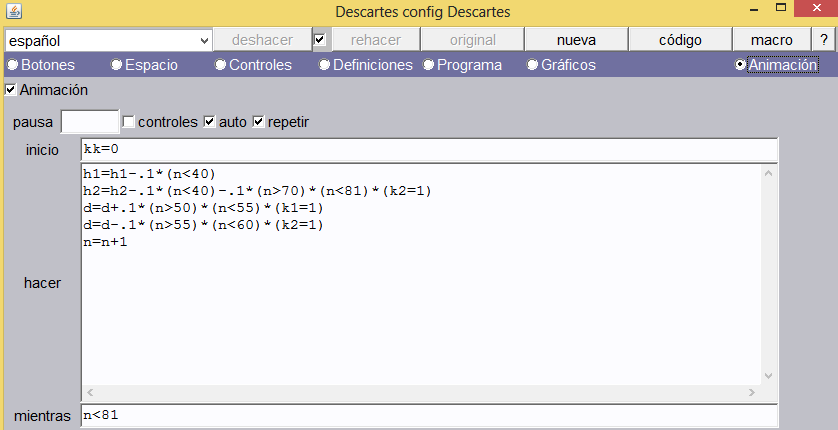
1Animación. Finalmente insertamos una animación tal como se indica en la imagen.
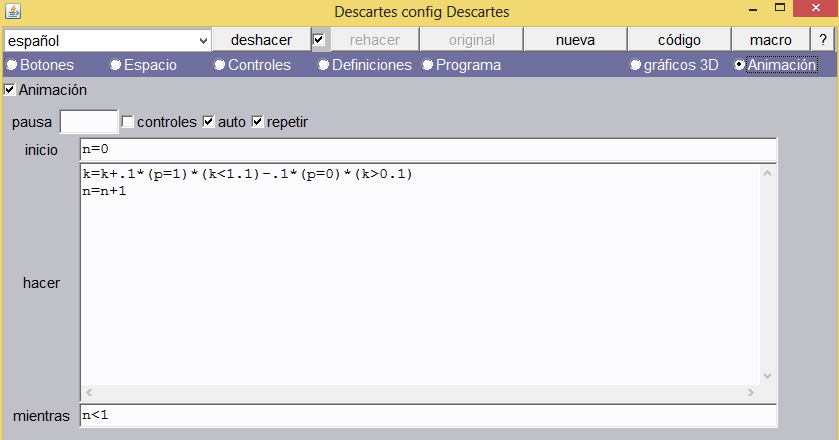
Analicemos la expresión k=k+.1*(p=1)*(k<1.1)-.1*(p=0)*(k>0.1). La variable k será incrementada en una décima, cuando P es igual a uno y k es menor que 1.1; es decir, el sumando .1*(p=1)*(k<1.1) tiene dos tipos de valor: 0.1 si las expresiones booleanas en paréntesis son verdaderas (.1*1*1) o 0 si alguna expresión booleana es falsa (.1*0*1 ó .1*1*0 ó .1*0*0). Análogamente funciona el decremento de k con el tercer sumando: -.1*(p=0)*(k>0.1). También podemos comprender la utilidad de los dos botones diseñados. A continuación, mostramos la escena final. Nos queda como tarea incluir los textos.
[1] El calificativo de selecto no es gratuito. Véase, por ejemplo, la tesis doctoral de Fleming sobre percepción de superficie.
[2] Oliva & Torralba (2007). Trends in Cognitive Sciences (2007), Vol. 11 No. 12, pág 520.
[3] Además de los demos, el grupo ha vinculado una gran cantidad de publicaciones que se pueden descargar fácilmente.
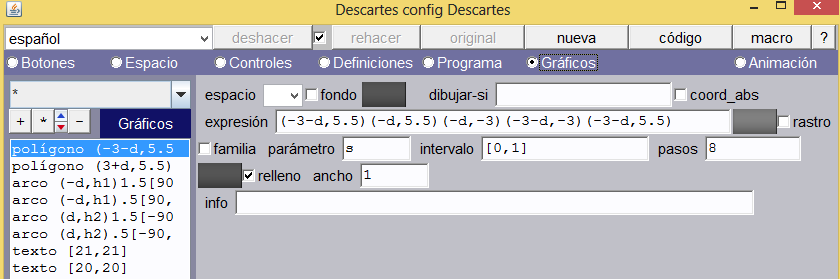
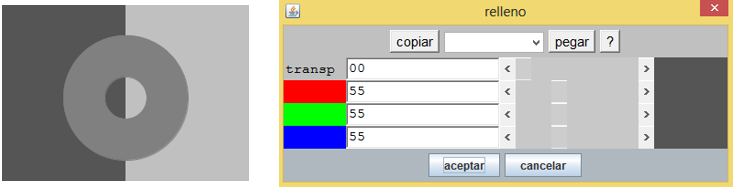
 El anillo. Lo construiremos con cuatro arcos para poder realizar las animaciones correspondientes. Habrá, entonces, dos arcos mayores y dos arcos menores. Los arcos menores tendrán un relleno igual al color del rectángulo donde se superponen (ver imagen derecha) y los arcos mayores un color gris uniforme.
El anillo. Lo construiremos con cuatro arcos para poder realizar las animaciones correspondientes. Habrá, entonces, dos arcos mayores y dos arcos menores. Los arcos menores tendrán un relleno igual al color del rectángulo donde se superponen (ver imagen derecha) y los arcos mayores un color gris uniforme.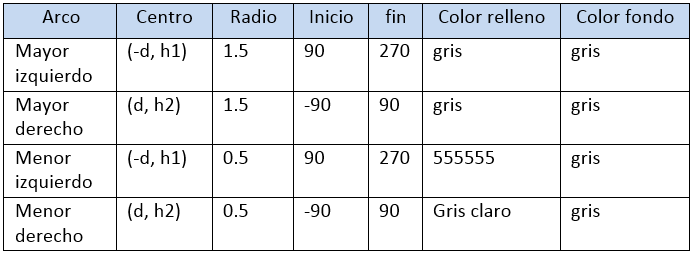

Comentarios recientes