En la siguiente escena tenemos un ejemplo de cómo se puede hacer con Descartes que un vídeo sea interactivo, es decir, que no sea sólo un instrumento de comunicación pasiva sino que requiera la participación activa del usuario.
-
Audios y vídeos interactivos con Descartes
(Puede descargar esta escena desde este enlace)En el siguiente documento tenemos una descripción de cómo se puede desarrollar esta escena: -
Animaciones
Una animación en Descartes es un algoritmo especial que refresca la escena cada vez que realiza un ciclo. Como todo algoritmo tiene la estructura inicio – hacer – mientras.
El Panel de configuración de la Animación tiene este aspecto.
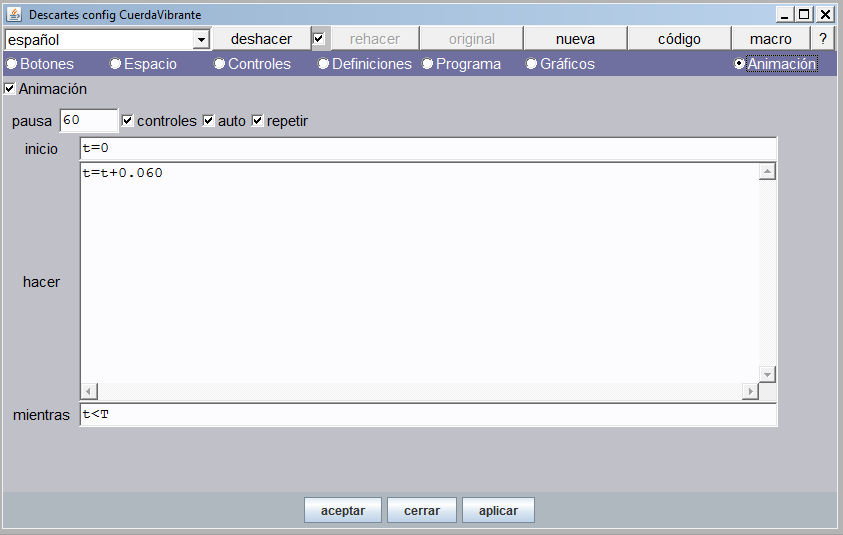
El panel de configuración de la animación tiene estos campos:
Animación
Activa o desactiva la animación.
Cuando el selector no está marcado los demás campos del panel están desactivados. Cuando el selector está activado todos los campos del panel se activan y el autor puede escribir en ellos o elegir opciones. Cuando la animación está activada, en la escena aparece un botón animar abajo a la derecha, con el que el usuario puede arrancar la animación, ordenar una pausa y continuar la animación.La etiqueta del botón alterna entre animar y pausapausa
El tiempo (en milisegundos) que el programa espera en cada paso de la animación.El valor por defecto es 60.
Los valores pequeños hacen que la animación sea más rápida y viceversa. En procesadores lentos los valores pequeños no necesariamente producen animaciones rápidas.
auto
Determina si la animación comienza automáticamente cuando la escena aparece en la pantalla y cada vez que se pulsa el botón de Inicio. Si el selector no está activado entonces para que comience es necesario que el desarrollador de la escena incluya algún evento u ofrezca un botón al usuario para que la active. repetir
Determina si la animación se repite indefinidamente o bien se detiene cuando la condición «mientras» deja de ser verdadera. inicio
Cálculos que se realizan al comenzar la animación.Puede incluir varias asignaciones separadas por «;”. hacer
Cálculos que se realizan en cada paso de la animación.Puede incluir varias asignaciones separadas por un salto de línea. mientras
Condición para que la animación continúe.Cuando esta condición deja de ser válida la animación se detiene o, si el selector «repetir» está activado, vuelve a comenzar. Los campos inicio, hacer y mientras funcionan igual que en cualquier algoritmo.
El siguiente ejemplo muestra una animación que representa una cuerda vibrante blanca con sus primeros armónicos en colores rojo, amarillo, verde, azul y los más altos en violeta. Para distinguir los de color violeta hay que aumentar mucho la amplitud.
(Puede descargar la escena anterior desde este enlace) -
Animaciones – Ejercicio
Descripción del ejercicio
Realizaremos un ejercicio que nos permitirá comprender cómo se anima una escena. Dicho ejercicio consiste en la construcción de una circunferencia unitaria (circunferencia goniométrica) y sobre ella un punto que se desplazará de acuerdo a un ángulo a que variará de 0 a 2pi Las coordenadas de este punto serán, entonces, (cos(a), sen(a)). Por otra parte, construiremos las funciones seno, coseno, tangente y secante, que serán animadas en función del ángulo a.
Primera animación. Circunferencia unitaria
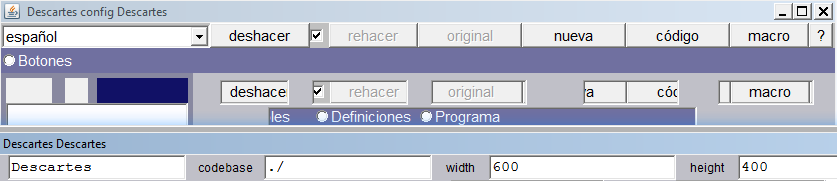
En primer lugar, definiremos el tamaño de la escena en 600×400 píxeles. Para ello, debemos recordar que este cambio se hace pulsando en la opción código.
Animación. Ahora, seleccionamos la opción animación, en la que incluiremos los valores que se observan en la imagen. Los valores el algoritmo sólo se pueden digitar si hemos activado la casilla de Animación.
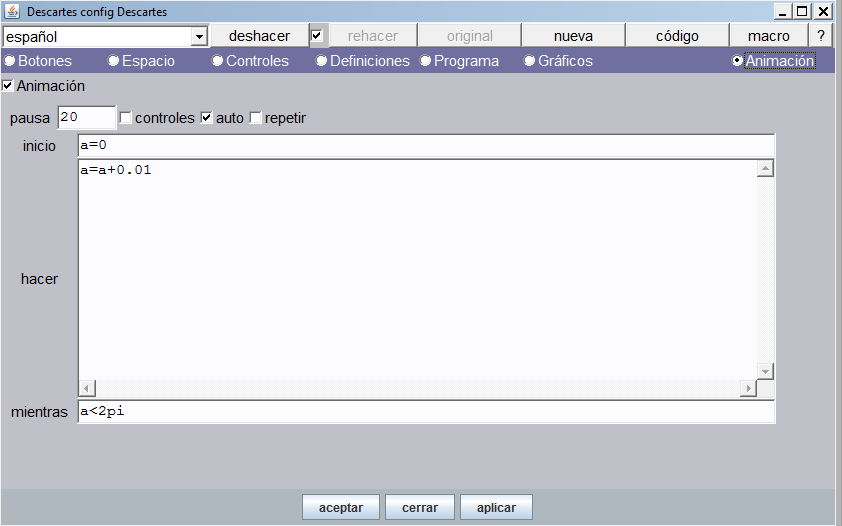
El contenido de la animación tiene la siguiente explicación:
- Pausa. Tiempo de espera entre un paso y otro de la animación. Por defecto está en 60 milésimas de segundo. Usaremos para este ejercicio un valor de 30.
- Inicio. Allí colocaremos nuestro ángulo a con un valor inicial de cero (0) radianes. Es posible “inicializar” varios parámetros separándolos por “;”. Por ejemplo: a=0; r=1;…
- Hacer. Aquí escribimos los cálculos de nuestra animación. En nuestro ejercicio, haremos que el ángulo se incremente en cada paso una centésima. Podríamos practicar con otros incrementos para observar los efectos sobre la animación.
- Mientras. Aquí escribimos la condición que permite que los pasos de “hacer” se sigan realizando. Es decir, mientras la condición sea verdadera, el ángulo se seguirá incrementando. En nuestro ejercicio la condición es a<2pi.
Circunferencia goniométrica animada. En la opción gráficos del editor de configuraciones, añadimos la circunferencia unitaria x2 + y2 = 1, tal como se observa en la imagen.
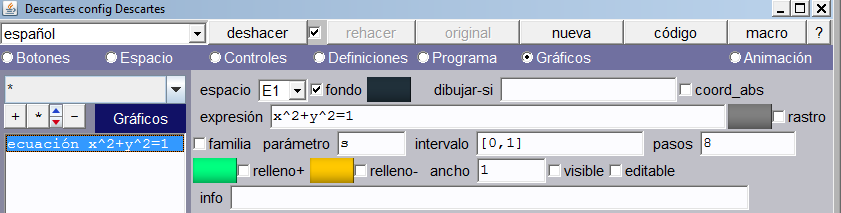
Haremos algunas modificaciones al espacio de trabajo, para efectos de una mejor visualización de la escena. Cambiamos la escala a 75 y la ubicación del origen de coordenadas en O.x = -35%.
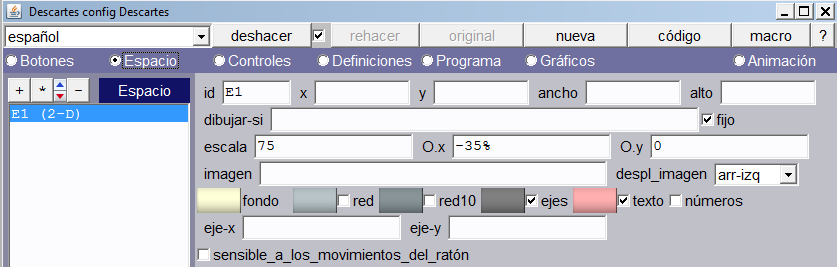
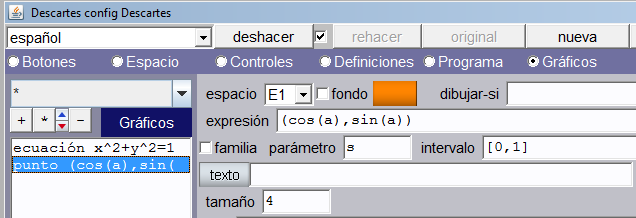
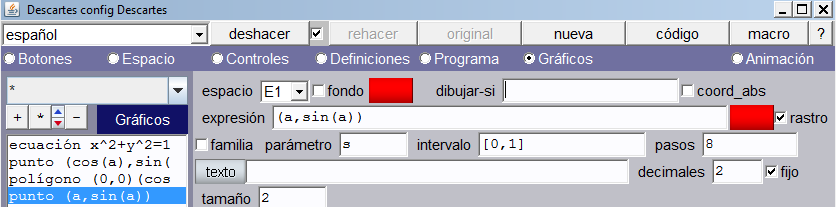
Nuevamente, en gráficos, añadiremos el siguiente punto: (cos(a), sin(a)), con color rojo y tamaño 5… ¡empieza la animación!
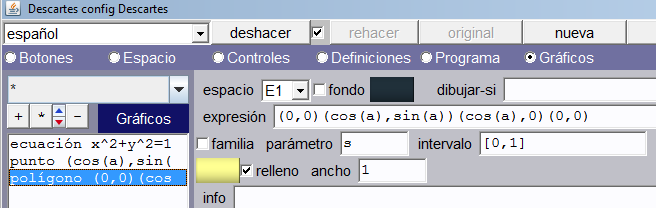
Triángulo trigonométrico animado. Ahora añadimos el siguiente polígono que nos animará el triángulo trigonométrico: (0,0)(cos(a),sin(a))(cos(a),0)(0,0). Observemos que hemos activado el color de relleno (podemos usar el color que deseemos).
Ahora, guardamos, ejecutamos y observamos esta primera animación.
Segunda animación. Funciones trigonométricas animadas
Vamos a animar la función seno añadiendo el siguiente punto (a, sin(a)). Para crear la animación activaremos la opción rastro con el color que queramos. Esta opción permite dejar la huella de los diferentes puntos que se dibujan con (a, sin(a)).
Como tarea, no queda incluir un control tipo menú para que muestre las demás funciones y un control tipo botón que pause o reanude la animación.
Esta sería la escena final
(Puede descargar la escena desde este enlace)Hemos incluido algo adicional, ¿qué es? Observemos la animación.
-
Animaciones – La ilusión de Adelson
ILUSIONES ANIMADAS
En este apartado aprenderemos sobre las ilusiones visuales del grupo de investigación sobre la Ciencia Perceptual del Instituto Tecnológico de Massachusetts (MIT) liderado por Edward Adelson.
Perceptual Science Group of the MIT. Este grupo fue creado en 1994 en el Departamento de Ciencias cognitivas y del Cerebro del MIT. El grupo se ha dedicado a la investigación de la percepción visual en brillo y transparencia, percepción de texturas, percepción de superficies, similitud perceptual, análisis de movimiento, entre otras líneas de investigación. El grupo está compuesto por cuatro profesores y un selecto grupo de estudiantes graduados o en curso[1]. Los investigadores principales son Edward Adelson (Profesor de Ciencias de la Visión), Richards Whitman (Profesor de Ciencias Cognitivas), Ruth Rosentholtz (Investigadora) y Aude Oliva (Profesora Asistente en Ciencias Visuales).
La profesora Oliva frente al tema de contexto expresa:
El contexto tiene efectos en múltiples niveles: semántico (una mesa y una silla se hallarán, probablemente en la misma imagen. No esperaríamos una mesa y un elefante), configuración espacial (un teclado se espera observarlo debajo de un monitor) y postura (Las sillas se esperan encontrar dirigidas hacia la mesa, una pluma de escribir esperamos verla en una posición particular respecto al papel y un auto debería estar orientado a los largo de una calle.[2]
Nuestro cerebro tiende a asociar los objetos percibidos con los conocimientos previos adquiridos. El contexto o entorno en el cual se encuentra el objeto hace que nuestro cerebro le asigne propiedades de ese contexto al objeto percibido. Es decir, no percibimos el color y brillo reales, sino los calculados en comparación con el color y brillo de los objetos cercanos (ver la ilusión de Neblina, por ejemplo). En la siguiente imagen, creada por Edward Adelson, las casillas A y B son del mismo tono gris. Diseñaremos un applet que evidencie la igualdad de color.

Algunos demos en flash se han publicado en http://web.mit.edu/persci/gaz/main-frameset.html, de los cuales hemos escogido la ilusión de Haze y el anillo de Koffka para diseñarlos en próximos apartados, pero ahora nos centraremos en la ilusión de Adelson[3].
Las animaciones múltiples en Descartes. El Nippe Descartes trae la opción de animación. En principio parece que sólo podemos realizar una sola animación; sin embargo, usando algunas expresiones de tipo booleano podemos lograr varias animaciones en una sola escena.
La ilusión del tablero ajedrezado
La ilusión de Adelson está compuesta de un tablero de 25 paralelepípedos, un cilindro y una sombra (shadow). El diseño de la escena lo haremos comenzando con la parte gráfica para terminar con las propiedades del espacio, las auxiliares y la animación.
Escena. Inicialmente, crearemos una escena de 550×400, en la que agregaremos, además, un espacio 3D con despliegue pintor y parámetros como los que indica la imagen.
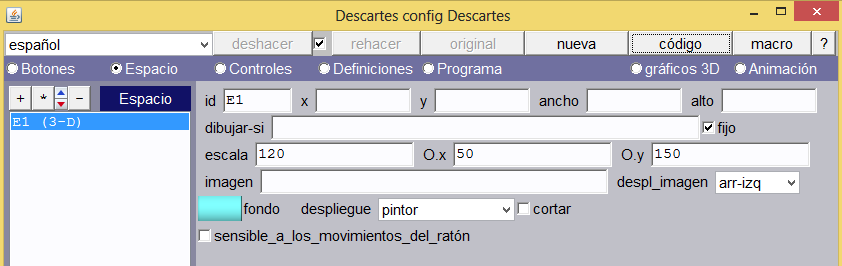
Gráficos. Inciaremos con la creación de los 25 paralelépipedos que se han numerado en la imagen siguiente. En la posición de los paralelépipedos 16, 17, 21 y 22 situaremos el cilindro.

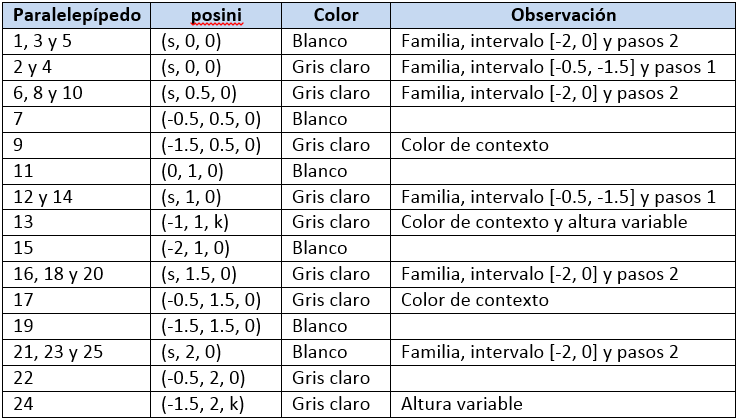
Paralelepípedos. Insertaremos estos prismas en el orden que se presenta en la tabla. Cada paralelepípedo tendrá un ancho y largo de 0.5 y un alto de 0.3, aristas activadas, sus colores serán alternados en gris claro y blanco, excepto en los colores de contexto.
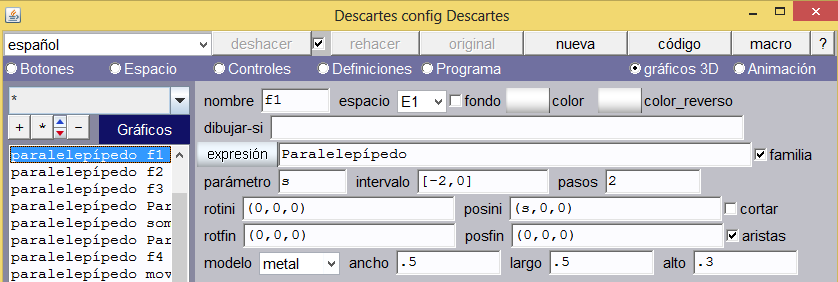
Aprovecharemos, en algunos paralelepípedos, la opción familia, que identificaremos por el posini y la observación; no obstante, debido a la animación, algunos serán construidos individualmente.
Observemos que los paralelepípedos 13 y 24 tendrán una altura variable, estos prismas serán los que animaremos posteriormente.
Cilindro. Insertemos un cilindro de color verde claro, ubicado en la posición (-3, 1.7, .65), con ancho y largo de 0.8, Nu = 40 y Nn = 1.
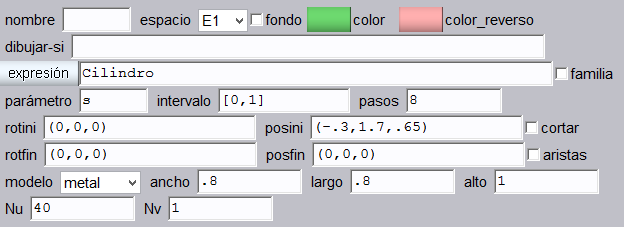
Tapa del cilindro. Añadimos la tapa del cilindro insertando un polígono regular (Polireg) en la posición (-.3, 1.7, 1.15), las demás propiedades de color, ancho, largo, Nu y Nv son iguales a las del cilindro.
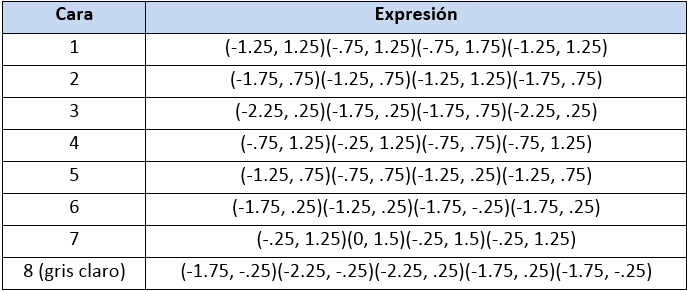
Caras de contexto (sombra). Para emular la sombra del cilindro sobre el tablero, insertaremos siete caras de color gris obscuro y una cara de color gris (extremo izquierdo de la imagen siguiente), cada cara tendrá un posini de (0, 0, 0.15).

Observemos que se trata de siete triángulos negros y un cuadrado gris claro. Analiza aparte las coordenadas de estos cuatro tipos de gráficos (paralelepípedo, polígono regular, cilindro y cara.
Segmentos. Añadimos dos segmentos de color rojo y naranja de acuerdo a las siguientes imágenes:
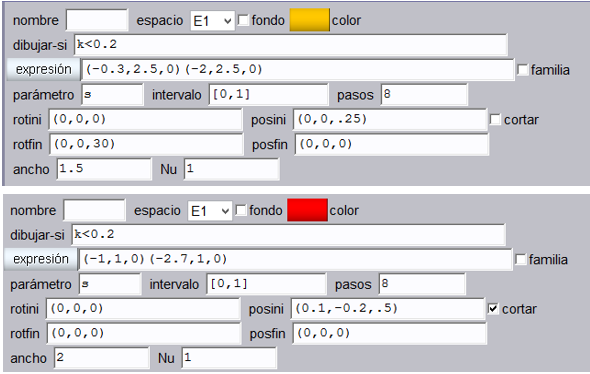
Los segmentos desaparecen cuando k empieza a aumentar en la animación.
Controles. Usaremos dos controles tipo botón. El primero tendrá como nombre Verificar y demás propiedades como aparecen en la imagen de abajo. El segundo botón tendrá las mismas propiedades excepto: nombre = Regresar, dibujar-si = k > 0.8 y parámetro p = 0. Los colores de los botones los podemos cambiar a nuestro gusto.
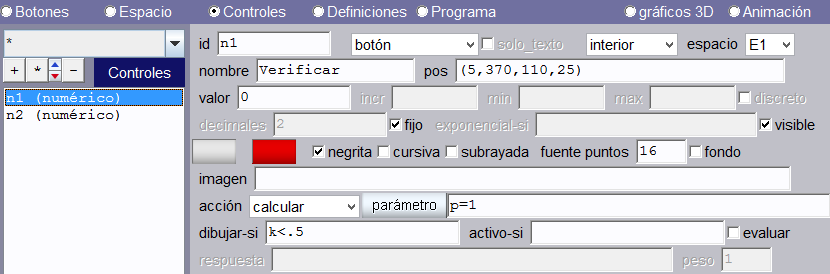
Algoritmo de inicio. Hemos usado dos variables para rotar el espacio E1.rot.y = 35 y E1.rot.z = 60.
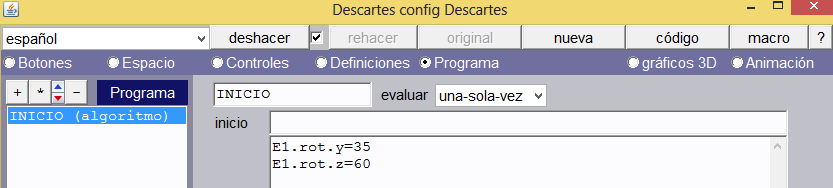
1Animación. Finalmente insertamos una animación tal como se indica en la imagen.
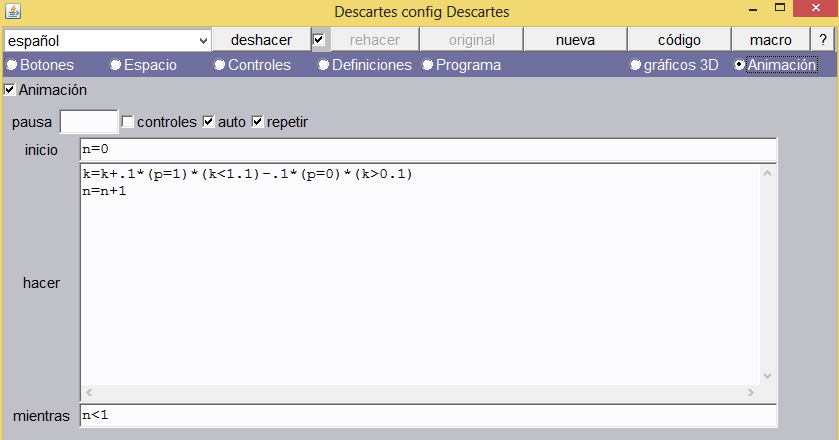
Analicemos la expresión k=k+.1*(p=1)*(k<1.1)-.1*(p=0)*(k>0.1). La variable k será incrementada en una décima, cuando P es igual a uno y k es menor que 1.1; es decir, el sumando .1*(p=1)*(k<1.1) tiene dos tipos de valor: 0.1 si las expresiones booleanas en paréntesis son verdaderas (.1*1*1) o 0 si alguna expresión booleana es falsa (.1*0*1 ó .1*1*0 ó .1*0*0). Análogamente funciona el decremento de k con el tercer sumando: -.1*(p=0)*(k>0.1). También podemos comprender la utilidad de los dos botones diseñados. A continuación, mostramos la escena final. Nos queda como tarea incluir los textos.
(Puede descargar esta escena y todas las de este artículo desde este enlace)
[1] El calificativo de selecto no es gratuito. Véase, por ejemplo, la tesis doctoral de Fleming sobre percepción de superficie.
[2] Oliva & Torralba (2007). Trends in Cognitive Sciences (2007), Vol. 11 No. 12, pág 520.
[3] Además de los demos, el grupo ha vinculado una gran cantidad de publicaciones que se pueden descargar fácilmente.
-
Animaciones – Las ilusiones de Koffka y de Haze
El anillo de Koffka
Esta ilusión la realizaremos utilizando tres animaciones.
Espacio. Creamos una escena de 600×400 y un espacio 2D, tal como aparece en la imagen.
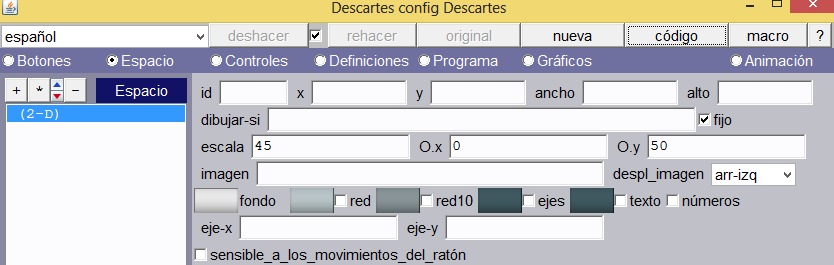
Controles. Usaremos tres controles interiores tipo botón (n1, n2, y n3): el primer botón (n1) es para iniciar la segunda animación (la primera se ejecuta al inicio de la escena), el segundo botón (n2) es para ejecutar la tercera animación y el tercero es un botón de inicio (regresa a la primera animación).
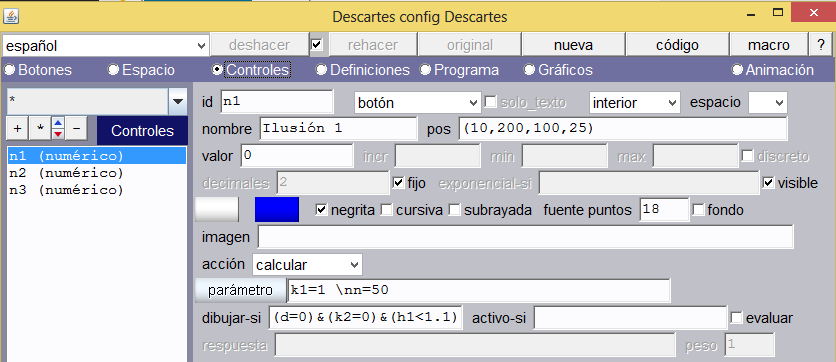
Botón Ilusión 1. Su configuración se muestra en la imagen anterior. Observemos que se dibuja si cumple con la siguiente condición: (d=0) & (k2=0) & (h1<1.1), donde d y h1 son variables de desplazamiento horizontal y vertical respectivamente, y k2 es una variable cuyos valores (0 ó 1) determinan si se inicia o no la animación dos. Los colores quedan a nuestra discreción.
Botón Ilusión 2. Tiene las mismas propiedades del anterior, excepto por el nombre (Ilusión 2), el color, el dibujar-si que es igual a (d>.3) & (k1=1) y el parámetro de cálculo que es k2=1 \nn=55.
Botón inicio. Tiene las mismas propiedades de los anteriores, excepto por el nombre (Inicio), el color, el dibujar-si que es igual a (h2<.1)&(k2=1) y el parámetro de cálculo que es k2=0 \nk1=0 \nn=0 \nd=0 \nh1=5 \nh2=5.[1]
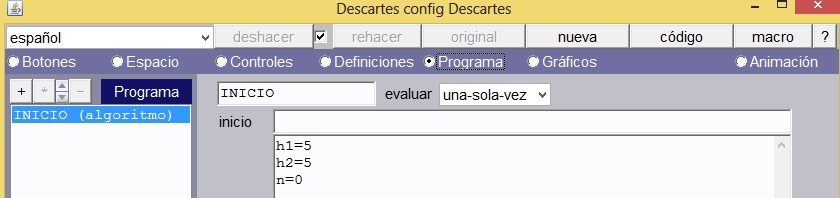
Algoritmo de inicio. Creamos tres variables: h1 = 5, h2 = 5 y n = 0. Las dos primeras las usaremos en la construcción de la gráfica y variarán en la animación. La última es una variable de control para las animaciones.
 Gráficos. Utilizaremos siete gráficos: dos polígonos, cuatro arcos y un texto.
Gráficos. Utilizaremos siete gráficos: dos polígonos, cuatro arcos y un texto.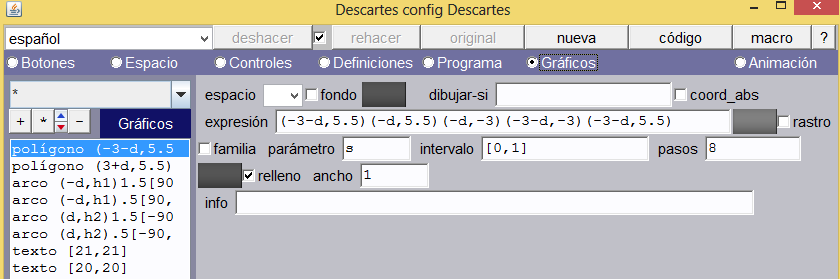
Polígonos. Corresponden a los dos rectángulos sobre los que se superpondrá el anillo de Koffka. El primero estará definido por las coordenadas:
(-3-d, 5.5)(-d, 5.5)(-d, -3)(-3-d, -3)(-3-d, 5.5)
Su color es la combinación RGB 555555 (ver imagen siguiente)[2].
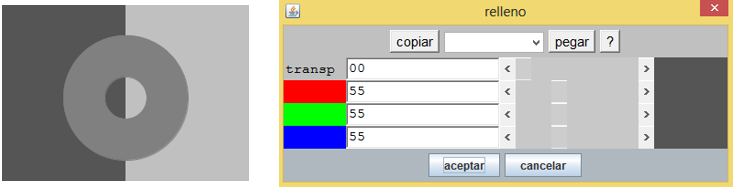
El segundo polígono (del lado derecho) estará definido por las coordenadas:
(3+d, 5.5)(d, 5.5)(d, -3)(3+d, -3)(3+d, 5.5) y color gris claro.
Observemos que los rectángulos incluyen, en su definición, la variable d. Eso significa que si d>0 entonces el primer polígono se desplazará a la izquierda y el segundo a la derecha.
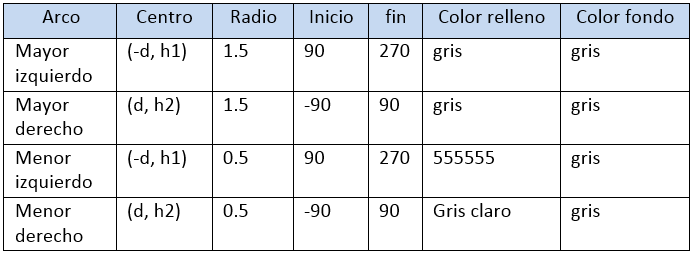
 El anillo. Lo construiremos con cuatro arcos para poder realizar las animaciones correspondientes. Habrá, entonces, dos arcos mayores y dos arcos menores. Los arcos menores tendrán un relleno igual al color del rectángulo donde se superponen (ver imagen derecha) y los arcos mayores un color gris uniforme.
El anillo. Lo construiremos con cuatro arcos para poder realizar las animaciones correspondientes. Habrá, entonces, dos arcos mayores y dos arcos menores. Los arcos menores tendrán un relleno igual al color del rectángulo donde se superponen (ver imagen derecha) y los arcos mayores un color gris uniforme.En la siguiente tabla se indican las propiedades de cada arco:
Observemos que los arcos dependen de la variable d para su desplazamiento horizontal y de las variables h1 y h2 para el desplazamiento vertical. En la primera y segunda animación h1 = h2 (ver escena al final de este apartado), en la tercera sus valores son diferentes.
El texto. Insertamos un texto para el título de la escena. El tamaño, tipo de letra y color, es a nuestra discreción.
Animaciones. Usaremos tres animaciones en una sola, utilizando controles booleanos. En la imagen siguiente podemos observar, inicialmente, que:
Se encuentran activadas las casillas Animación, auto y repetir. Esta activación es parte clave para nuestras animaciones. Auto permite que la escena se inicie con la primera animación y repetir permite que el ciclo hacer – mientras se repita indefinidamente. Es decir, n inicia en cero y se incrementa hasta un valor de 80; luego se repite continuamente este proceso.
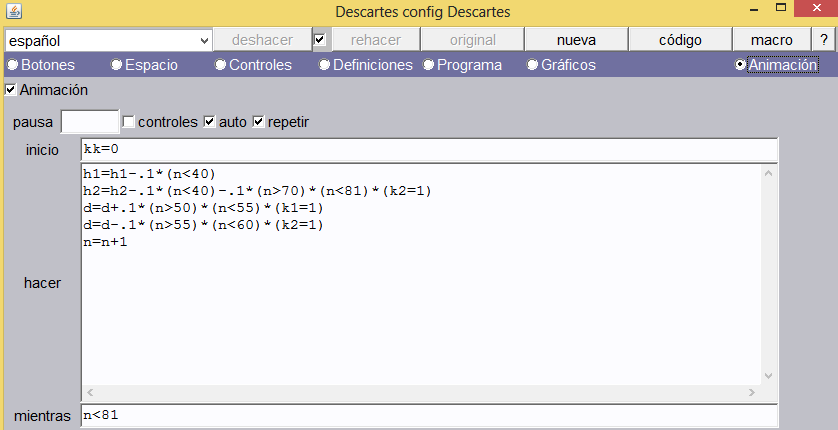
Durante la ejecución de los ciclos se realizan las siguientes animaciones:
Animación 1. Esta animación se logra a través de las instrucciones:
h1=h1-.1*(n<40)
h2=h2-.1*(n<40)-.1*(n>70)*(n<81)*(k2=1)
Recordemos que definimos h1 = h2 = 5 y n = 0, esto significa que los arcos se encuentran en la ordenada cinco. Al ser verdadera la expresión n<40, entonces, durante el primer proceso de auto animación los valores de h1 y h2 se reducirán en una décima por cada ciclo, hasta que n sea igual a 40; es decir, los valores de h1| y h2 se reducirán en 40*.1 = 4, hasta quedar en la ordenada uno. La animación consiste en deslizar verticalmente hacia abajo el anillo de Koffka. Cada vez que hagamos clic en el botón inicio, h1 y h2 volverán a tomar el valor de cinco y n el de cero, repitiendo la animación.
Animación 2. Esta animación se logra a través de la instrucción:
d=d+.1*(n>50)*(n<55)*(k1=1)
El valor de la variable d se incrementa cuando k1 = 1; es decir, cuando hacemos clic sobre el botón “Ilusión 1”. Este incremento es sólo de cinco décimas ¿por qué?
Animación 3. Esta animación es más interesante, en tanto que junta de nuevo arcos y polígonos y, desplaza la segunda mitad del anillo hacia abajo. Se logra a través de las instrucciones:
h2=h2-.1*(n<40)-.1*(n>70)*(n<81)*(k2=1)
d=d-.1*(n>55)*(n<60)*(k2=1)
Observemos que la variable d vuelve a recuperar las cinco centésimas perdidas en la animación anterior y que h2 se reduce en la misma cantidad. Si analizamos con cuidado ambas instrucciones, notaremos que:
- Las reducciones de d y h2 se ejecutan cuando k2 =1; es decir, cuando se hace clic sobre el botón “Ilusión 2”.
- Primero se reduce la variable d y luego empieza a descender la segunda parte del anillo.
Finalmente, observemos la escena:
(Puede descargar la escena anterior desde este enlace)La ilusión de neblina de Haze
Esta ilusión se ha diseñado utilizando los conceptos anteriores: familias de polígonos, arcos y animaciones. Proponemos, como tarea, estudiarla y tratar de reproducirla. Si se presentan problemas, podemos copiar editar la escena para analizar la forma como fue diseñada. A continuación, se presenta la escena:(Puede descargar la escena anterior desde este enlace)
[1] Recuerda que RGB significa Red Green Blue (Rojo, Verde y Azul)
[2] Recuerda que los cálculos definidos en parámetro se pueden ingresar haciendo clic en el botón parámetro ó sobre el mismo cuadro de diálogo separando cada cálculo con la expresión \n (barra inclinada inversa + n).

Comentarios recientes