El anillo de Koffka
Esta ilusión la realizaremos utilizando tres animaciones.
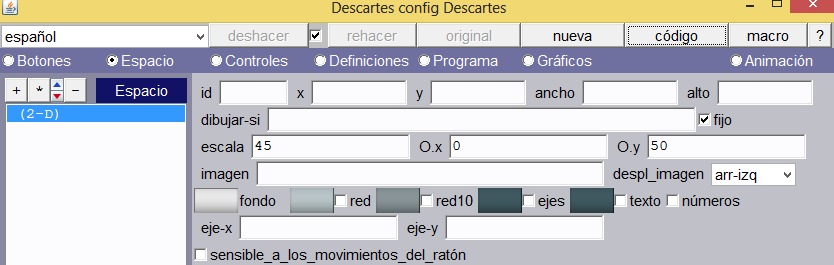
Espacio. Creamos una escena de 600×400 y un espacio 2D, tal como aparece en la imagen.
Controles. Usaremos tres controles interiores tipo botón (n1, n2, y n3): el primer botón (n1) es para iniciar la segunda animación (la primera se ejecuta al inicio de la escena), el segundo botón (n2) es para ejecutar la tercera animación y el tercero es un botón de inicio (regresa a la primera animación).
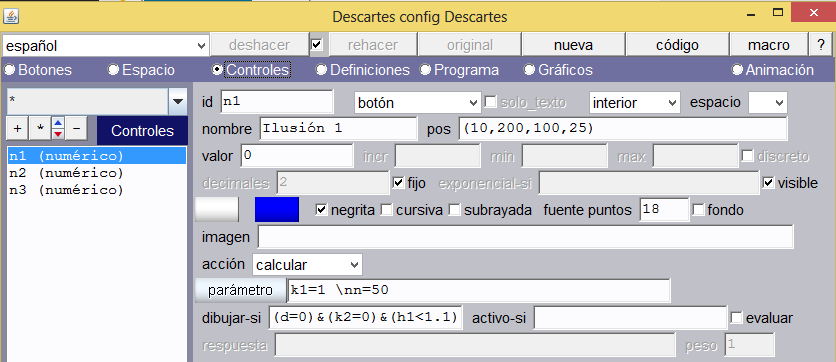
Botón Ilusión 1. Su configuración se muestra en la imagen anterior. Observemos que se dibuja si cumple con la siguiente condición: (d=0) & (k2=0) & (h1<1.1), donde d y h1 son variables de desplazamiento horizontal y vertical respectivamente, y k2 es una variable cuyos valores (0 ó 1) determinan si se inicia o no la animación dos. Los colores quedan a nuestra discreción.
Botón Ilusión 2. Tiene las mismas propiedades del anterior, excepto por el nombre (Ilusión 2), el color, el dibujar-si que es igual a (d>.3) & (k1=1) y el parámetro de cálculo que es k2=1 \nn=55.
Botón inicio. Tiene las mismas propiedades de los anteriores, excepto por el nombre (Inicio), el color, el dibujar-si que es igual a (h2<.1)&(k2=1) y el parámetro de cálculo que es k2=0 \nk1=0 \nn=0 \nd=0 \nh1=5 \nh2=5.[1]
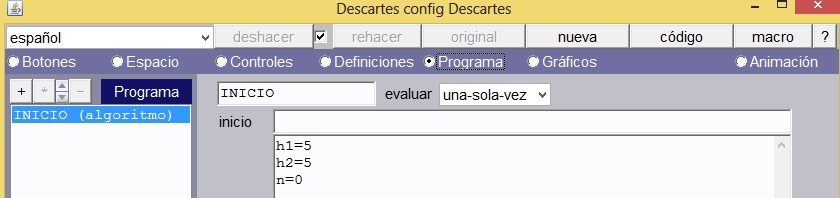
Algoritmo de inicio. Creamos tres variables: h1 = 5, h2 = 5 y n = 0. Las dos primeras las usaremos en la construcción de la gráfica y variarán en la animación. La última es una variable de control para las animaciones.
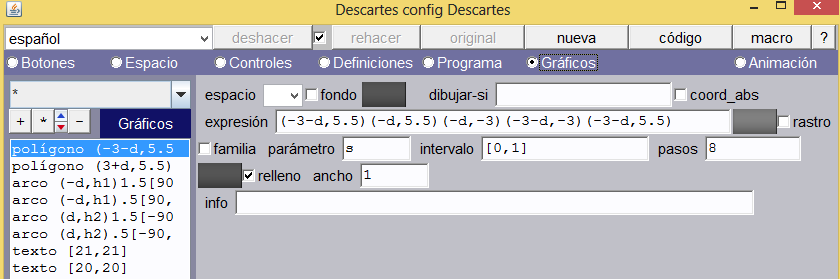
Polígonos. Corresponden a los dos rectángulos sobre los que se superpondrá el anillo de Koffka. El primero estará definido por las coordenadas:
(-3-d, 5.5)(-d, 5.5)(-d, -3)(-3-d, -3)(-3-d, 5.5)
Su color es la combinación RGB 555555 (ver imagen siguiente)[2].
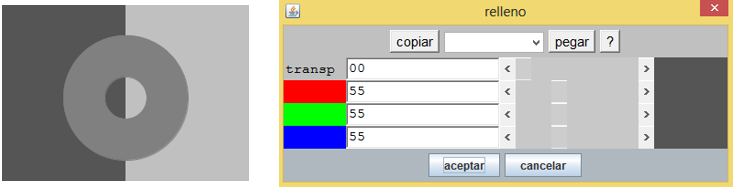
El segundo polígono (del lado derecho) estará definido por las coordenadas:
(3+d, 5.5)(d, 5.5)(d, -3)(3+d, -3)(3+d, 5.5) y color gris claro.
Observemos que los rectángulos incluyen, en su definición, la variable d. Eso significa que si d>0 entonces el primer polígono se desplazará a la izquierda y el segundo a la derecha.
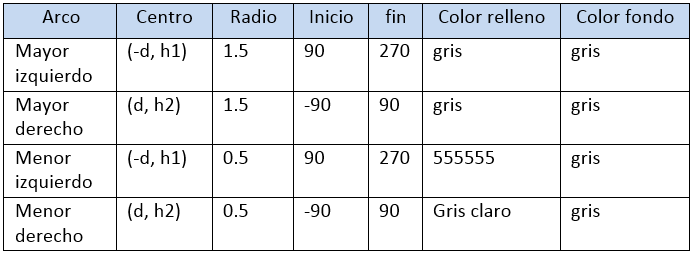
 El anillo. Lo construiremos con cuatro arcos para poder realizar las animaciones correspondientes. Habrá, entonces, dos arcos mayores y dos arcos menores. Los arcos menores tendrán un relleno igual al color del rectángulo donde se superponen (ver imagen derecha) y los arcos mayores un color gris uniforme.
El anillo. Lo construiremos con cuatro arcos para poder realizar las animaciones correspondientes. Habrá, entonces, dos arcos mayores y dos arcos menores. Los arcos menores tendrán un relleno igual al color del rectángulo donde se superponen (ver imagen derecha) y los arcos mayores un color gris uniforme.
En la siguiente tabla se indican las propiedades de cada arco:
Observemos que los arcos dependen de la variable d para su desplazamiento horizontal y de las variables h1 y h2 para el desplazamiento vertical. En la primera y segunda animación h1 = h2 (ver escena al final de este apartado), en la tercera sus valores son diferentes.
El texto. Insertamos un texto para el título de la escena. El tamaño, tipo de letra y color, es a nuestra discreción.
Animaciones. Usaremos tres animaciones en una sola, utilizando controles booleanos. En la imagen siguiente podemos observar, inicialmente, que:
Se encuentran activadas las casillas Animación, auto y repetir. Esta activación es parte clave para nuestras animaciones. Auto permite que la escena se inicie con la primera animación y repetir permite que el ciclo hacer – mientras se repita indefinidamente. Es decir, n inicia en cero y se incrementa hasta un valor de 80; luego se repite continuamente este proceso.
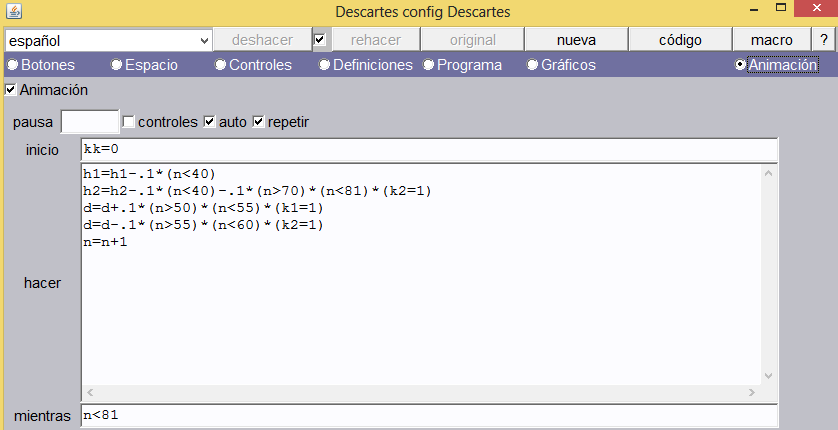
Durante la ejecución de los ciclos se realizan las siguientes animaciones:
Animación 1. Esta animación se logra a través de las instrucciones:
h1=h1-.1*(n<40)
h2=h2-.1*(n<40)-.1*(n>70)*(n<81)*(k2=1)
Recordemos que definimos h1 = h2 = 5 y n = 0, esto significa que los arcos se encuentran en la ordenada cinco. Al ser verdadera la expresión n<40, entonces, durante el primer proceso de auto animación los valores de h1 y h2 se reducirán en una décima por cada ciclo, hasta que n sea igual a 40; es decir, los valores de h1| y h2 se reducirán en 40*.1 = 4, hasta quedar en la ordenada uno. La animación consiste en deslizar verticalmente hacia abajo el anillo de Koffka. Cada vez que hagamos clic en el botón inicio, h1 y h2 volverán a tomar el valor de cinco y n el de cero, repitiendo la animación.
Animación 2. Esta animación se logra a través de la instrucción:
d=d+.1*(n>50)*(n<55)*(k1=1)
El valor de la variable d se incrementa cuando k1 = 1; es decir, cuando hacemos clic sobre el botón “Ilusión 1”. Este incremento es sólo de cinco décimas ¿por qué?
Animación 3. Esta animación es más interesante, en tanto que junta de nuevo arcos y polígonos y, desplaza la segunda mitad del anillo hacia abajo. Se logra a través de las instrucciones:
h2=h2-.1*(n<40)-.1*(n>70)*(n<81)*(k2=1)
d=d-.1*(n>55)*(n<60)*(k2=1)
Observemos que la variable d vuelve a recuperar las cinco centésimas perdidas en la animación anterior y que h2 se reduce en la misma cantidad. Si analizamos con cuidado ambas instrucciones, notaremos que:
- Las reducciones de d y h2 se ejecutan cuando k2 =1; es decir, cuando se hace clic sobre el botón “Ilusión 2”.
- Primero se reduce la variable d y luego empieza a descender la segunda parte del anillo.
Finalmente, observemos la escena:
La ilusión de neblina de Haze
[1] Recuerda que RGB significa Red Green Blue (Rojo, Verde y Azul)
[2] Recuerda que los cálculos definidos en parámetro se pueden ingresar haciendo clic en el botón parámetro ó sobre el mismo cuadro de diálogo separando cada cálculo con la expresión \n (barra inclinada inversa + n).

Haz un comentario