Una matriz es un arreglo bidimensional de constantes. Si M es una matriz entonces M[i,j] es el elemento que está en la columna i+1 y en la fila j+1. Observe que la convención adoptada en Descartes no es la usual en la literatura matemática, es decir, el primer subíndice referencia al número de columna y el segundo al número de fila, lo que equivale a que Descartes trabaja internamente con la matriz traspuesta. También los subíndices se numeran desde 0, por tanto el número de fila y columna es uno más del que indica el subíndice respectivo.
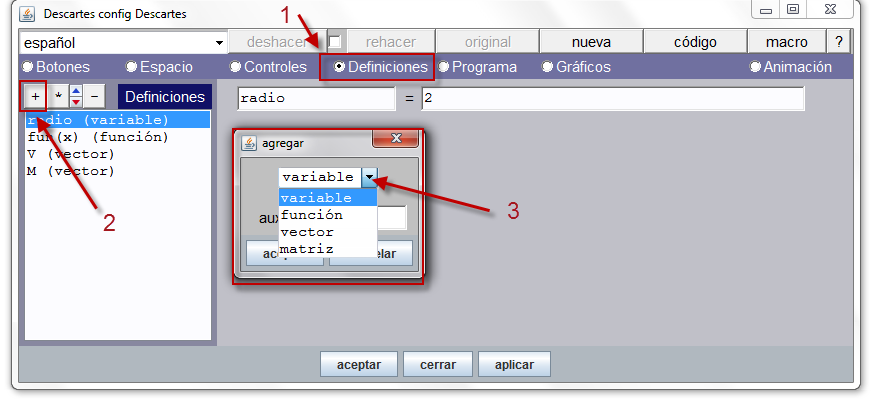
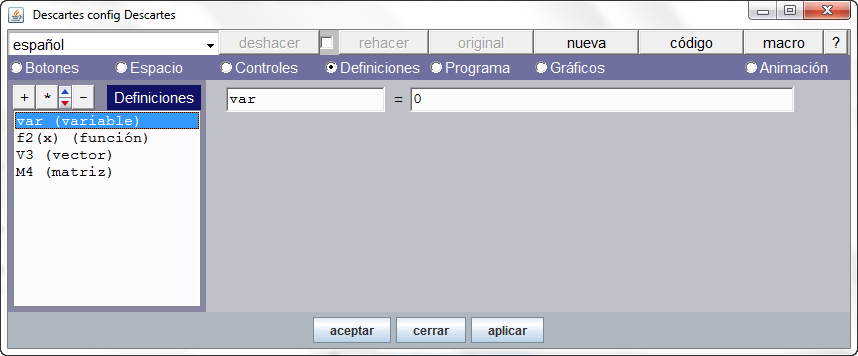
El panel de configuración de una matriz se muestra en la siguiente figura.
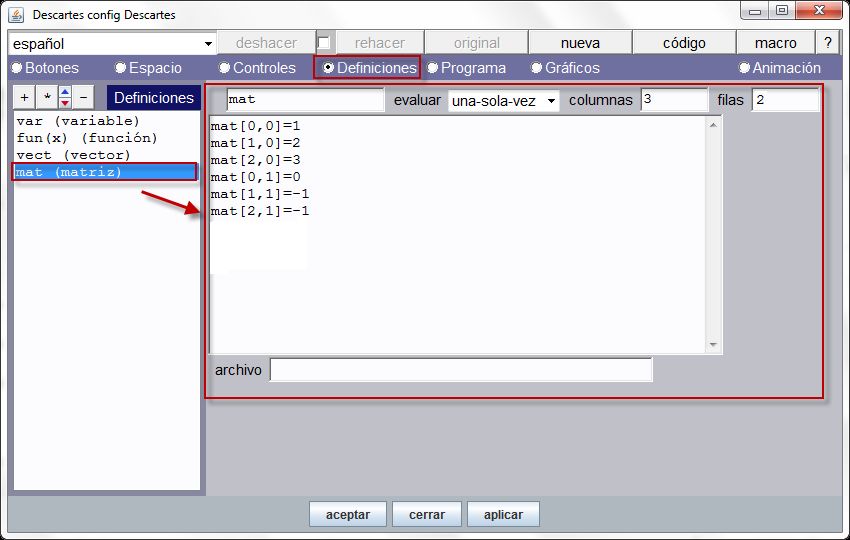
Matriz con 2 filas y 3 columnas
El caso ahí reflejado se corresponde con una matriz de 3 columnas y 2 filas
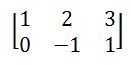
matriz con la que se desea trabajar
cuya identificación interna es mat. Y según el criterio indicado el elemento mat[1,0]=2 es el que está ubicado en columna 2 (1+1=2) y en la fila 1 (0+1=1) , es decir, internamente Descartes guarda la matriz traspuesta de la anterior:
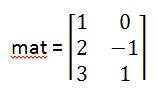
Matriz guardada por Descartes según la notación usual
Los campos específicos para configurar una matriz son los siguientes:
- Identificador de la matriz a través del cual se puede referenciar.
- evaluar que puede tomar los valores «una-sola-vez» o «siempre» y hace que el vector tome los valores indicados en el campo de texto de inicialización sólo cuando se inicie la escena o cada vez que haya una interacción con la misma. Este parámetro ha quedado restringido a «una sola vez» en la versión 5, la actualización «una vez» cuando los valores se realizan mediante variables o cuando se desea «siempre» se realiza repectivamente usando los algoritmos Inicio y Cálculos.
- columnas. Es el número de columnas de la matriz.
- filas. Es el número de filas de la matriz
- Área de texto. Es un campo de texto donde pueden escribirse asignaciones a los valores de la matriz, separadas por saltos de línea o por ;
Por ejemplo, en la imagen anterior el identificador de la matriz es mat y tiene 3 columnas y 2 filas y sus elementos se definen como:
mat[0,0]=1
mat[1,0]=2
mat[2,0]=3
mat[0,1]=0
mat[1,1]=-1
mat[2,1]=1
- archivo. Este parámetro no está operativo para matrices. Para una carga dinámica de una matriz a partir de un fichero es necesario utilizar funciones según se describe en el artículo ficheros y matrices.
El área de texto que aparece en el panel de configuración de una matriz sirve para asignar valores a (o inicializar ) los elementos de la matriz. El contenido del área de texto que se ofrece por defecto contempla una asignación a todos elementos del valor 0, no obstante los elementos no inicializados de un vector tienen por defecto ese valor.
Para inicializar una matriz no es necesario utilizar el área de texto, también se puede utilizar un algoritmo descrito en una función algorítmica o bien mediante un fichero. Estas dos últimas formas son las más aconsejables cuando la matriz tiene muchos elementos. En la siguiente escena se muestra un ejemplo de estas posibilidades.
Si se desea ver cómo está realizado el objeto anterior puede descargarse desde aquí .
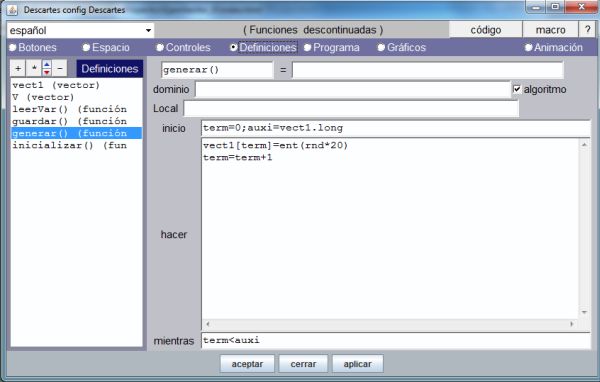
En la escena anterior la opción de menú etiquetada como “Generar” permite asignar a cada elemento de una matriz denominada matr1 un valor aleatorio mediante una función que está reflejada en la siguiente imagen. En ella un ciclo que se ejecuta desde 0 hasta el número de columnas de dicha matriz (3 en este caso) asigna a cada uno de los elementos de cada fila (matr1[term,0] y matr1[term,1]) un número aleatorio en el intervalo [0, 20)
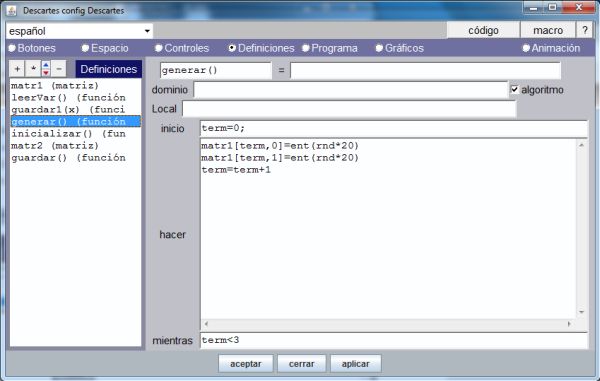
Código para inicializar una matriz con valores aleatorios mediante una función algorítmica
En el artículo ficheros y matrices puede aprenderse cómo asignar valores a una matriz mediante el uso de ficheros y en él se describe cómo en la escena anterior se realiza esa asignación.
![]()

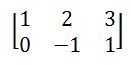
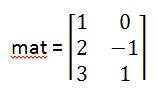



Comentarios recientes